【数据结构与算法】查找算法（一）

一、概论

1.1 基本概念

查找（searching）就是根据给定的某个值，在查找表中确定一个其关键字等于给定制的数据元素（或记录）。

查找表（search table）是由同一类型的数据元素（或记录）构成的组合。例如下图：

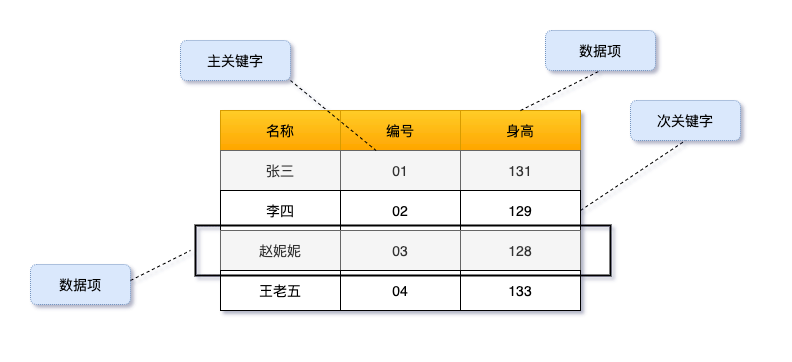
关键字（key）三数据元素中某个数据项的值，又称为键值。用它可以标示一个记录的某个数据项，我们称为关键码。

1.2 分类

按照表查找方式来分有辆大众：静态查找表和动态查找表。

静态查找表（Static Search Table）： 只做查找操作的查找表，主要操作有：

1. 查询某个“特定的”数据元素是否在查找表中
2. 检索某个“特点的“数据元素和各种属性

动态查找表（Dynamic Search Table）：在查找的过程中同时插入查找表中不存在的数据元素，或者从查找表中删除已经存在的某个数据元素。动态查找表的操作是两个：

1. 查找时插入数据元素
2. 查找时删除数据元素

二、静态查找

2.1 顺序查找

顺序查找（Sequential Search）又叫线性查找，是最基本的查找技术，他的查找过程是：从表的第一个（或最后一个）记录开始，逐个进行记录的关键字和给定值比较，

1. 若某个记录的关键字和给定值相等，则查找成功，找到所查的记录；
2. 如果直到最后一个（或第一个）记录，其关键字和给定值比较都不等时，则表中没有所查的记录，查找不成功。

2.3.1 顺序查找算法

算法比较简单，在数组里遍历查找:

int Sequential_Search(int *a, int n, int key)
{
    int i;
    for (i = 1; i<= n; i++) {
        if (a[i] == key) {
            return i;
        }
    }
    return 0;
}

2.3.2 顺序查找优化

由于上述算法，每次都需要判断i是否越界，稍显复杂，我们对算法进行改进，在0位加入一个哨兵，可以减少一次让 i 与 n 比较，具体如下：

int Sequential_Search(int *a, int n, int key)
{
    int i;
    // 1. 在0 位设置称为key，称为哨兵
    a[0] = key ;
    i = n;
    
    // 2. 从尾部开始倒序循环
    while (a[i] != key) {
        i--;
    }
    // 3. 返回>0 说明找到虚序号；=0 则 = key，表示查找失败
    return i;
}

这里改动了3个步骤

1. 在0 位设置称为key，称为哨兵
2. 循环倒置。从尾部开始倒序循环，好处是形成了一个完整循环（包括哨兵）
3. 查找结果二合一：返回>0 说明找到虚序号；=0 则 = key，表示查找失败

2.4 折半查找

折半查找（Binary Search），又称为二分查找。

前提是线性表中的记录必须是关键码有序（通常从小到大有序），线性表必须采用顺序存储。

折半查找的基本思想：

• 在有序表中，去中间记录作为比较对象，若给定值与中间记录的关键字相等，则查找成功；
• 若给定值小于中间记录的关键字，则在中间记录作伴去继续查找；
• 若给定值大于中间记录的关键字中，则在中间记录的右半区继续查找。

不断重复上述过程直到查找成功，或所有查找区域无记录，查找失败位置。

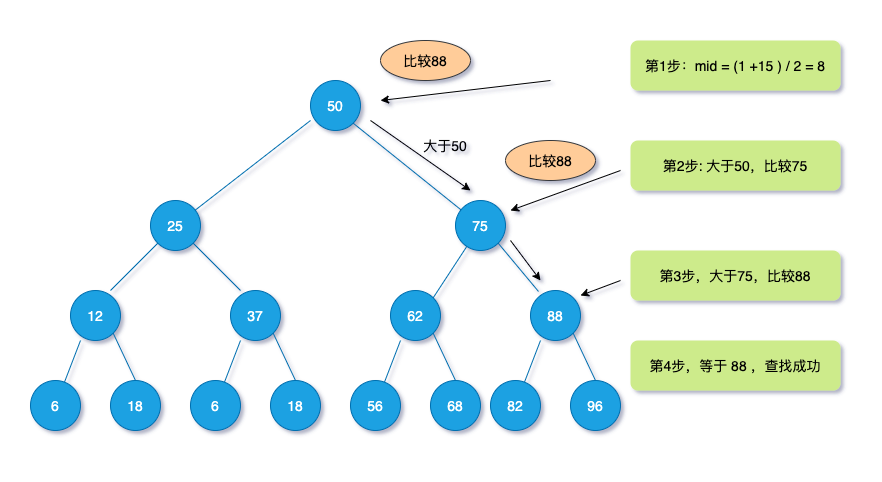
举例：现在有个数组 $<!–swig20–>$，查找其中 $88$ 的序号

代码实现如下：

// 折半查找
int Binary_Search(int *a, int n, int key)
{
    int low, high, mid;
    low = 1;
    high = n;
    while (low <= high) {
        mid = (low + high) / 2;
        if (key < a[mid]) {
            high = mid - 1;
        }else if(key > a[mid]){
            low = mid + 1;
        }else{
            return mid;
        }
    }
    return 0;
}

查找流程如下图:

2.3 插值查找

2.3.1 折半改进

由于折半查找会从中间开始查找，一旦超过一定量级，查找任务还是比较繁重。所以考虑是否还有改进空间

查找代码中求 mid的计算公式可以改进为：

$$
mid = \frac{low+high}{2} = low + \frac{1}{2} (high - low)
$$
也就是 mid等于最下标 low 加上 最高下标 high 与low 的差值的一半。

考虑将这个一半改进为以下方案：
$$
mid = low + \frac{ key - a [low]}{ a[high] - a[low]}(high - low)
$$
改进的好处：可以大大减少查找的次数。

比如数组 {6,12,18,25,31,37,43,50,56,62,68,75,82,88,96}，查找18 ，按照折半查找需要查找4步才可以找到

使用新公示，需要 $\frac{ key - a [low]}{a[high] - a[low]}$ = $ \frac{(18 - 12)}{(96 - 12)} \approx 0.071$，那么此时 $mid\approx 1 + 0.071\times (15-1) = 1.994$，取整后，只需要查询2次即可，大大提升了效率。

这样的到了另一种有虚表查找算法，插值查找法。

2.3.2 核心概念

插值查找法(Interpolation Search) 是根据要查找的关键字key 与查找表中最大最小记录的关键字比较后的查找方法，其核心就在于插值公示:
$$
\frac{key - a[low]}{a[high] - a[low]}
$$
缺点：不适合数字差距不均匀的数组。如 {0, 1, 2, 1000, 30000}

2.3.2 算法实现

由上可知，只需要改进一行代码

  // 插值查找
int Binary_Search(int *a, int n, int key)
{
    int low, high, mid;
    low = 1;
    high = n;
    while (low <= high) {
    		//  插值公示
        mid = low + (high - low) * (key - a[low]) / (a[high] - a[low]));
        if (key < a[mid]) {
            high = mid - 1;
        }else if(key > a[mid]){
            low = mid + 1;
        }else{
            return mid;
        }
    }
    return 0;
}

2.5 斐波那契查找

斐波那契查找（Fibonacci Search），利用了黄金分割来实现。

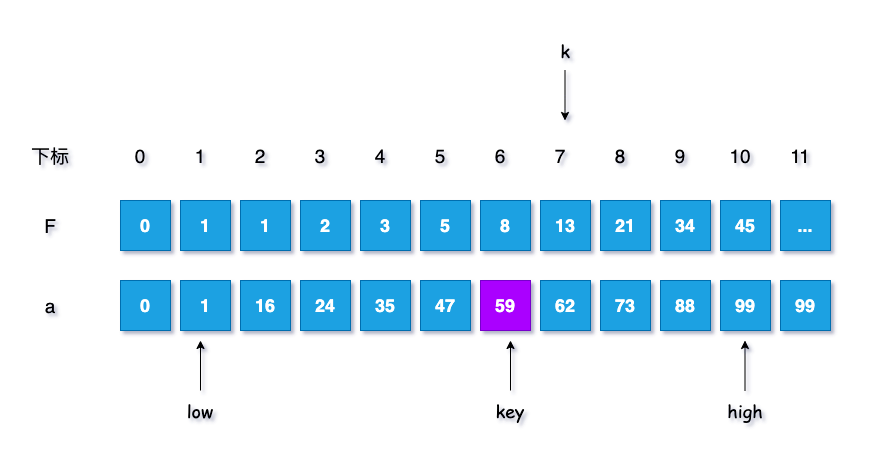
查找的流程，先举例实现吧，假设给定一个数组 $a[10] = $ {0, 1, 16, 24, 35, 47, 59, 62,73, 88, 99}, 此时$n = 10$，需要查找的键为 $key = 99$

• 先定义一个斐波那契数列 F[n]

  下标	0	1	2	3	4	5	6	7	8	9
  F	0	1	1	2	3	5	8	13	21	34

  它原理之前有学习过，实现原理是递归原理，代码实现如下：

  F[0] = 0;
  F[1] = 1;
  for (int i = 2; i < 100; i++) {
      F[i] = F[i -1] + F[i - 2];
  }

• 定义变量和下表

  int low, high, mid, i, k;
  low = 1, high = n;

  其中 low 、high分别为数组最低下标，默认 high为最大

  

• 计算 n 位于斐波那契数列的位置

  while (n > F[k]) -1
  	k++;

  由于上文给出的数组长度$n = 10$，得出 $F[6] < n < F[7]$， 所以此时 $k = 7$，在队列中如图示

  

• 将不满的数值补全，用a[n]，为什么补齐？

  for (i = n; i < F[k] - 1; i++) {
      a[i] = a[n];
  }

• 开始查找：

  1. 设定初始条件 $low <= high$，假设查找 n = 10，需要查找key = 59

  2. 计算当前分割下标，$mid = low + F[k - 1] -1$， 此时$mid = 1 + F[7-1] -1 =8$

  3. 判断，若 $key < a[mid]$ ，即如果查找记录小于当前分割记录

     • 最高下标调整到分隔下标的 $mid -1$ 处

       high = mid -1;

     • 斐波那契数列下标减$1$位

       k--;

     这一步中 key 为59， a[mid] 及a[8] 为73，所以$key<a[mid]$，需要进行调整， 如下图所示

     

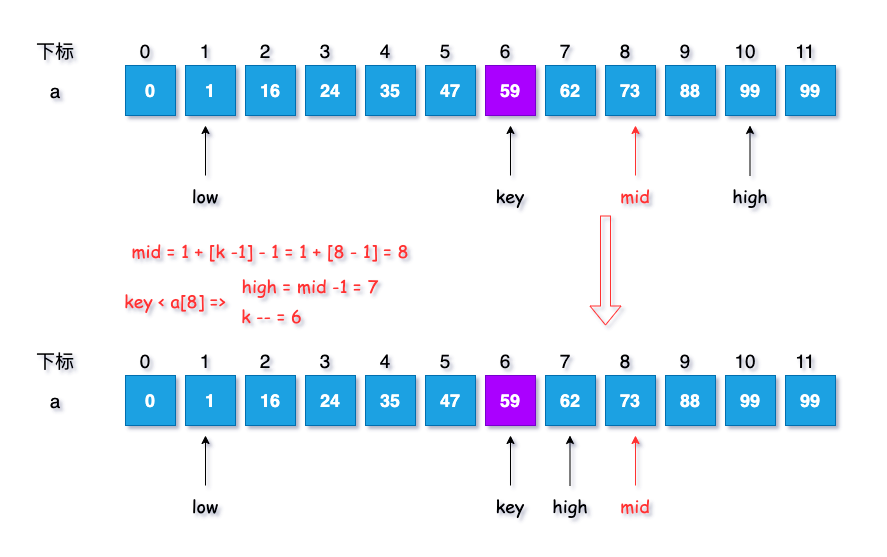
     此时各项参数结果为：$k = 6, low = 1, mid = 8, high = 7$

  4. 继续循环查找。

     1. 计算当前分隔的下标：$mid = F[6-1] - 1 = 5$ 。
     2. 继续判断 key 与 a[mid]，此时 $a[5] = 47 < key$，
     3. 执行两个步骤：

     • 最低下标调整到分割下标 $mid + 1$ 处

       low = mid + 1;

     • 斐波那契数列下标减2位

       k = k - 2;

     实现示意图如下：

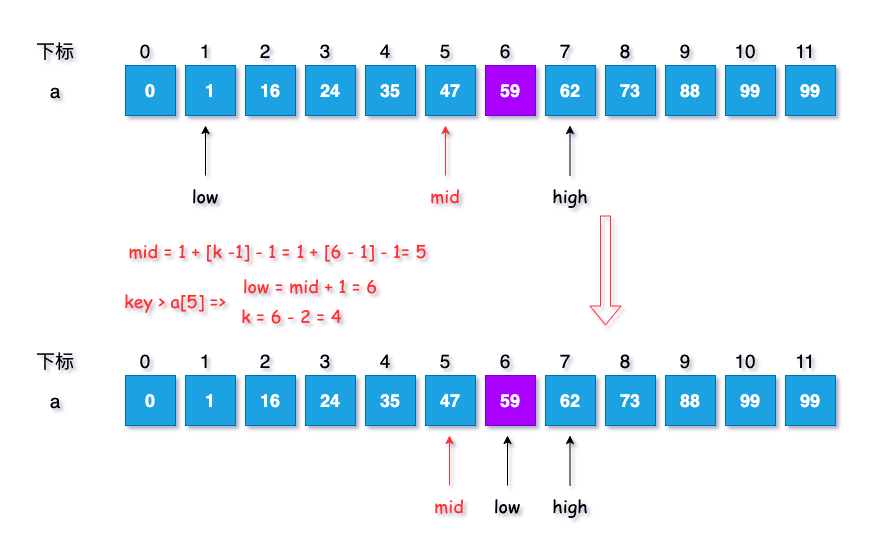
     此时各项参数结果为：$k = 4, low = 6, mid = 5, high = 7$

  5. 再次循环。

     1. 计算当前分隔的下标：$mid = 6 + F[4-1] -1 = 7$。
     2. 继续判断 key 与 a[mid] 的大小，此时 $a[7] = 62 > key$，因此执行第三步的策略。
     3. 重复一下如下：

     • 最高下标调整到分隔下标的 $mid -1$ 处

       high = mid -1;

     • 斐波那契数列下标减$1$位

       k--

     实现示意图如下：

     

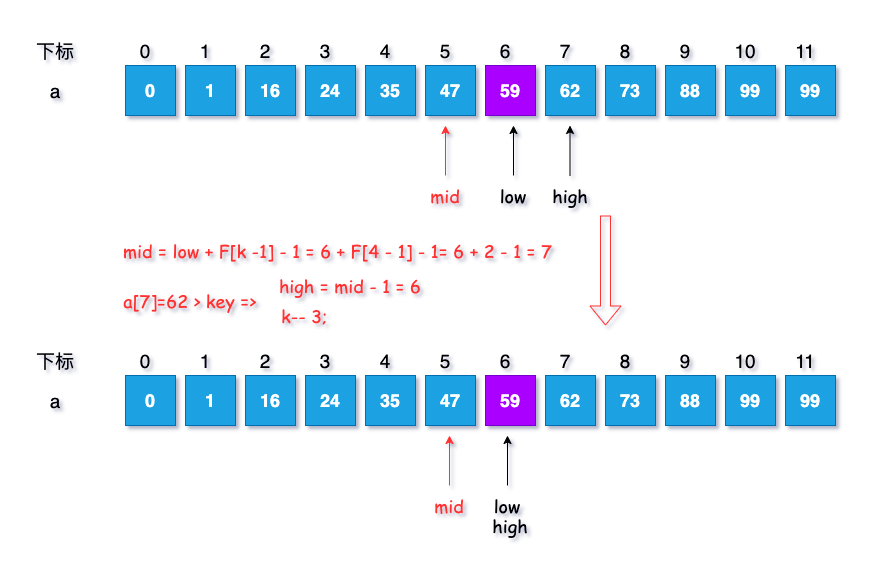
     此时各项参数结果为：$k = 3, low = 6, mid = 5, high = 6$

  6. 再次循环。

     1. 计算当前分隔的下标：$mid = 6 + F[3-1] =1 = 6$

     2. 判断 key 与 a[mid] ，此时 a[6] = 59 = key 。说明查找到，进行返回数组下标，返回值为 $6$

        if(mid < n)
        	return mid;
        else
        	return n;

• 回答为什么补齐$a[n]$

  在循环查找的过程中，如果查找的$key=99$，

  那么第一次查找时，

  • $mid = 8$；
  • $low = mid + 1 = 9$
  • $k = k - 2 = 7 - 2 = 5$

  第二次循环时，此时改变分隔mid 下标的值，$mid =low + F[k - 1] - 1 = 9 + 3 - 1 = 11$， 而此时a[mid] 为a[11] ，数组a 中的11位时没有值，会导致下一步与 key 的比较失败，为了避免情况发生，对上文中将不满的数值补全，用 a[i] = a[n]。

2.2.2 算法核心

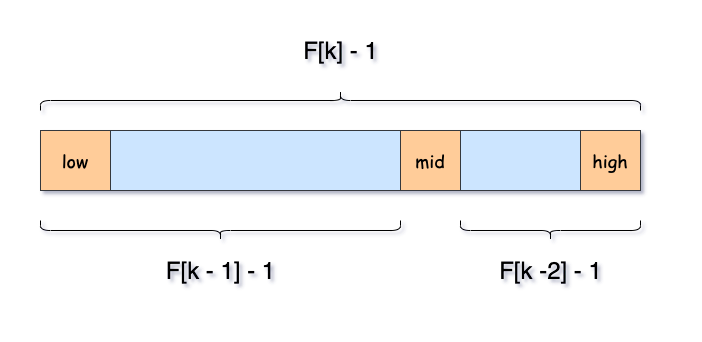
根据上文的查找流程，总结一下算法核心

1. 当 $key = a[mid]$ 时，查找成功
2. 当 $key < a[mid]$ 时，新范围是第 low 个到第 mid -1 个，此时范围个数为 F[k - 1] - 1 个
3. 当 $key > a[mid]$ 时，新范围是第 m+1 个到第 high 个，此时范围个数为 F[k-2] -1 个

示意图如下：

2.2.2 算法实现

先看看代码

int F[100];
int Fibonnaci_Search(int *a, int n, int key)
{
    int low, high, mid, i, k;
    low = 1;
    high = n;
    k = 0;
    while (n > F[k] - 1) {
        k++;
    }
    for (i = n; i < F[k] - 1; i++) {
        a[i] = a[n];
    }
    
    while (low <= high) {
        mid = low + F[k -1] -1;
        if (key < a[mid]) {
            high = mid -1;
            k--;
        }
        else if (key > a[mid])
        {
            low = mid++;
            k = k -2;
        }
        else
        {
            if (mid <= n)
                return mid;
            else
                return n;
        }
    }
    return 0;
}

2.6 查找效率

三种查找方式的公式如下，三种方式各有优劣，适合不同场景:

• 折半查找: $mid = (low + high) / 2$
• 插值查找，适合: $mid = low + \frac{key - a[low]}{a[high] - a[low]} * (high - low)$
• 斐波那契查找: $mid = low + F[k - 1] - 1$

优劣点即使用场景：

• 折半查找：适合数据规模较小，执行效率高
• 插值查找：适合数据规模较大，比折半查找更高效，但规模较小，以数值递增波动较大时与折半查找区别不大；
• 斐波那契：相比插值查找，适合数据递增波动较大的场景。

三、动态查找

3.1 二叉排序树

3.1.1 定义

二叉排序树（Binary Sort Tree），又称为二叉查找树。它是一种空树，或者具有下列性质的二叉树：

• 若它的左子树不空，则右子树上所有结点的值均小于它的根结点的值
• 若它的右子树不空，则左子树上所有结点的值均大于它的根结点的值
• 它的左、右子树分别为二叉排序树

3.1.2 查找

1. 二叉树的结构如下：

   typedef struct BitNode{
       int data;												 // 数据域
       struct BitNode *lChild, *rChild; // 指针分别指向左、右子树
   }BitNode, *BiTree;

2. 代码实现如下:

   Status SearchBST(BiTree T, int key, BiTree f, BiTree *p)
   {
       if (!T) {
           *p = f;
           return FALSE;
       }else if( key == T->data){
           *p = T;
           return SUCCESS;
       }else if(key < T->data){
           return SearchBST(T->lChild, key, T, p);
       }else{
           return SearchBST(T->rChild, key, T, p);
       }
   }

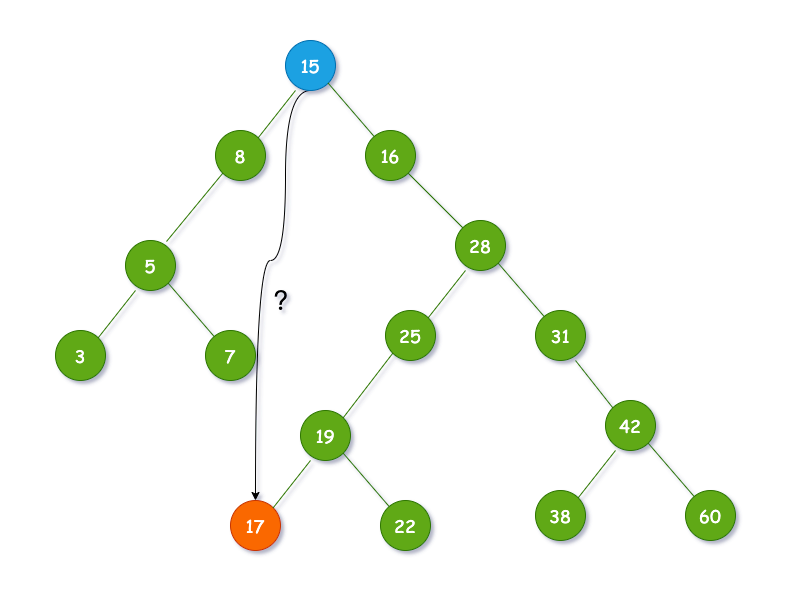
3. 分析查找流程:

   1. 判断树的有效性
   2. 指针 f 指向 T 结点的双亲，如果第一次，使用值为 NULL
   3. 判断结点数值与 目标值元素结点的数据是否相等
      1. 结点的值与目标值相等——指针 p 指向元素结点，返回成功
      2. 如果目标值key小于元素结点数据，在左子树上，进行查找函数递归
      3. 如果目标 key大于元素结点数据，在右子树上，进行查找函数递归

4. 示意图如下：

   

   

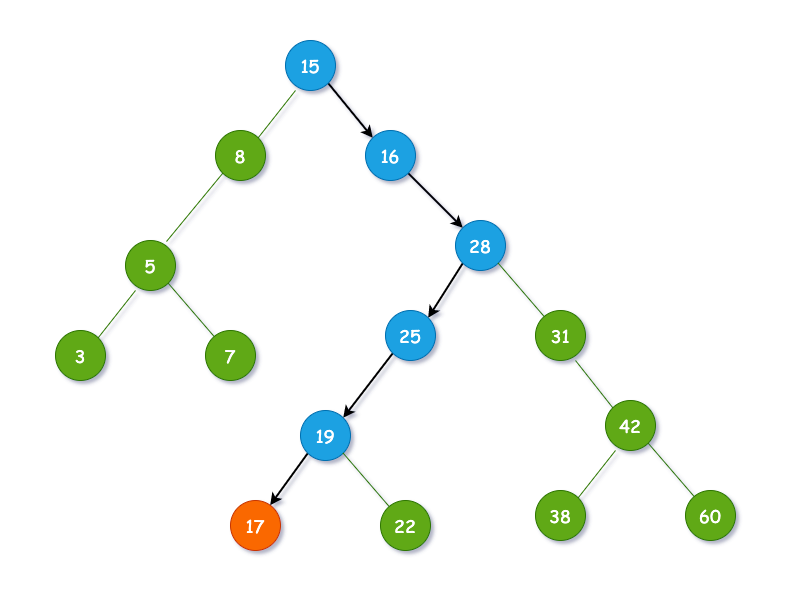
3.1.3 插入

插入的流程有以下几个步骤

• 先查找目标元素，如果存在，无需插入，返回
• 如果不存在，判断 目标值 key 与 指针p
  • 如果大于，则 插入 s 为左孩子
  • 如果小于，则插入 s 为右孩子

代码实现如下

Status InsertBST(BiTree *T, int key)
{
    BiTree p, s;
    if (!SearchBST(*T, key, NULL, &p)) {
        s = (BiTree)malloc(sizeof(BiTree));
        s->data = key;
        s->lChild = s->rChild = NULL;
        if (!p) {
            *T = s;
        }else if (key < p->data){
            p->lChild = s;
        }else{
            p->rChild = s;
        }
        return SUCCESS;
    }else{
        return FALSE;
    }
}

3.2.4 删除

删除结点有三种情况分析:

• 叶子结点
• 仅有左/右子树的结点
• 左右子树都有结点的

对应的策略如下：

• 当删除叶子结点：

  无需操作，free 即可

• 当删除仅有左/右子树的结点时：

  将它的原子树移动到它的位置，替代他即可

• 当删除结点左右子树都有结点时：

  • 找到待删结点的前缀
  • 重接q 的右子树
  • 重接q 的左子树

代码实现如下：

Status DeleteBST(BiTree *p)
{
    BiTree q,s;
    // 右子树为空
    if ((*p)->rChild == NULL) {
        q = *p;
        *p = (*p)->lChild;
        free(q);

    // 左子树为空
    }else if ((*p)->lChild == NULL){
        q = *p;
        *p = (*p)->rChild;
        free(q);
        
    // 左右子树均不为空
    }else{
        q = *p;
        s = (*p)->lChild;
        while (s->rChild) {
            q = s;
            s = s->rChild;
        }
        (*p)->data = s->data;
        if (q!= *p) {
            q->rChild = s->lChild;
        }else{
            q->lChild = s->lChild;
        }
        free(s);
    }
    return SUCCESS;
}

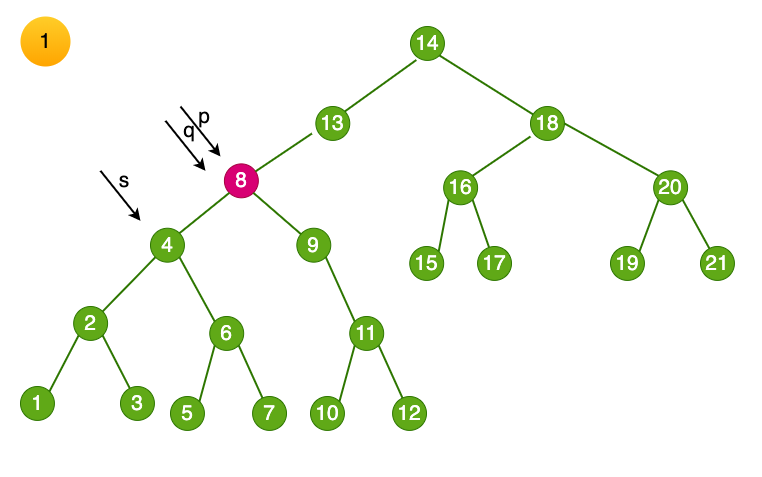
示意图如下：

• 找到目标结点 $8$，标记为 p
• 将p 赋值给临时变量 q，再将其左子树赋值给临时变量 s

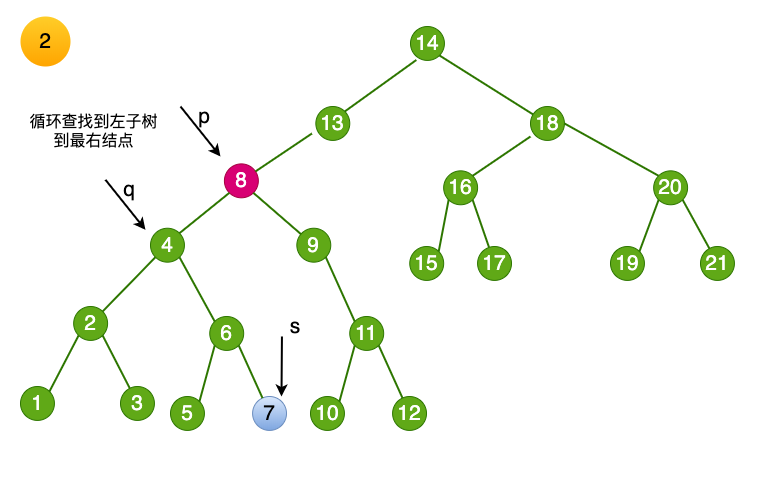
• 循环找到左子树的右结点，知道右侧尽头，得到结点$7$，将临时变量s指向该结点

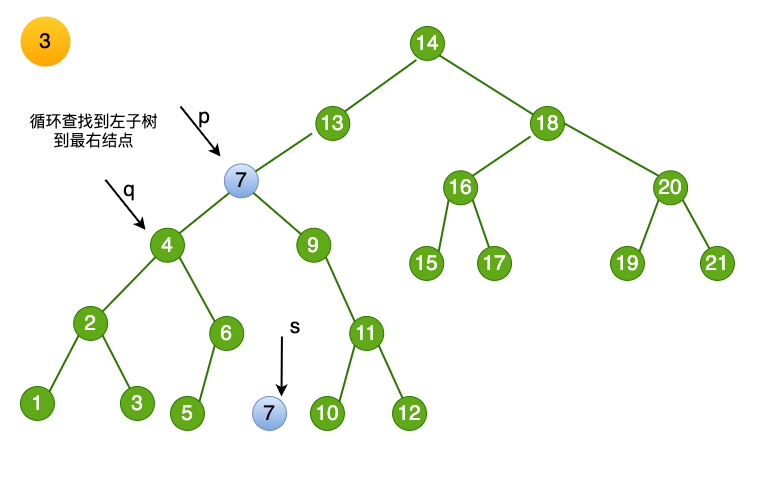
• 将删除结点的数值赋值为 临时变量 s-> data，即 p->data = s->data。

• 最后一步，将目标结点7 进行释放，至此，删除完成。

上述情况时最右侧结点为叶子结点，还有一种情况最右侧结点右子结点，该如何处理呢。

• 这里的步骤和上文一样，赋值临时变量p，s

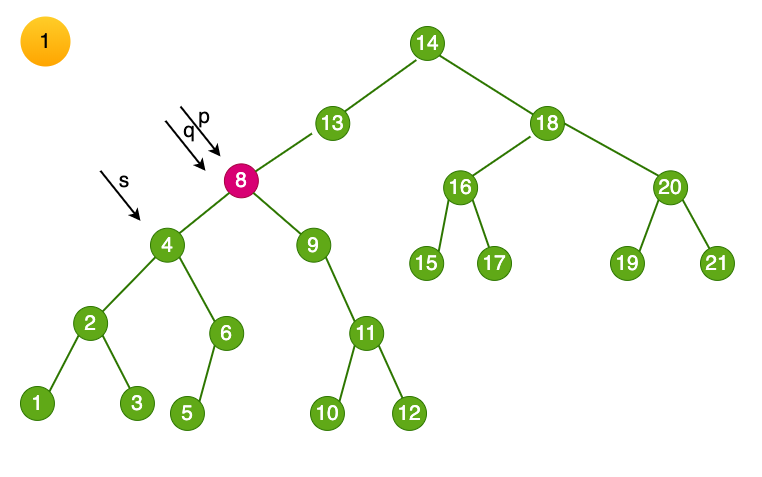
• 找到目标结点6，将临时变量s 指向6

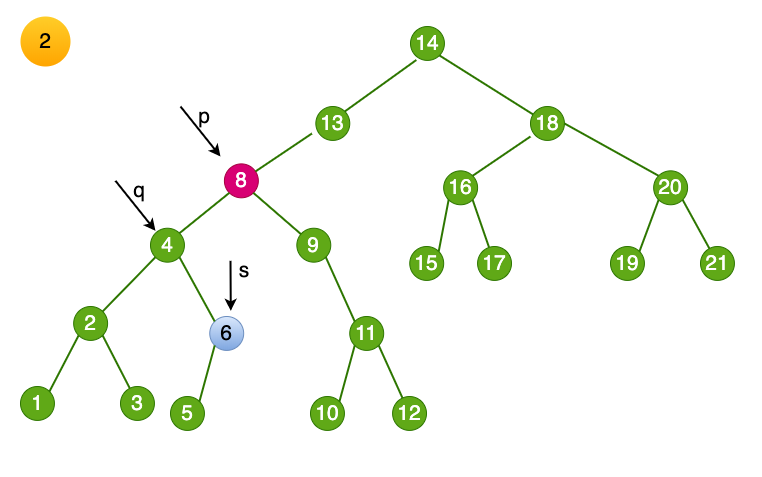
• 将删除结点的数值赋值为 临时变量 s-> data，即 p->data = s->data。此时相当于结点6 被删除，它的子结点需要妥善处理。

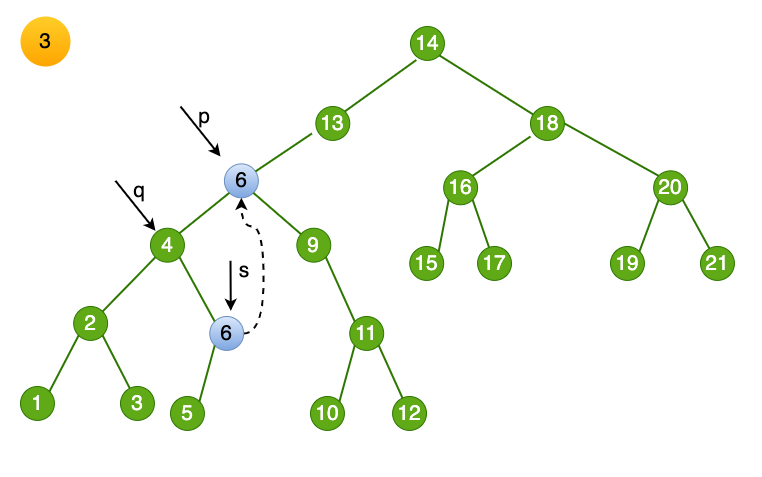
• 此时如果 p 和 q 指向不相同，则将 6 的子树交给 它的父结点。

  即 q->rChild = s->lChild。这样节点6 留下的左结点被链接进入树了。

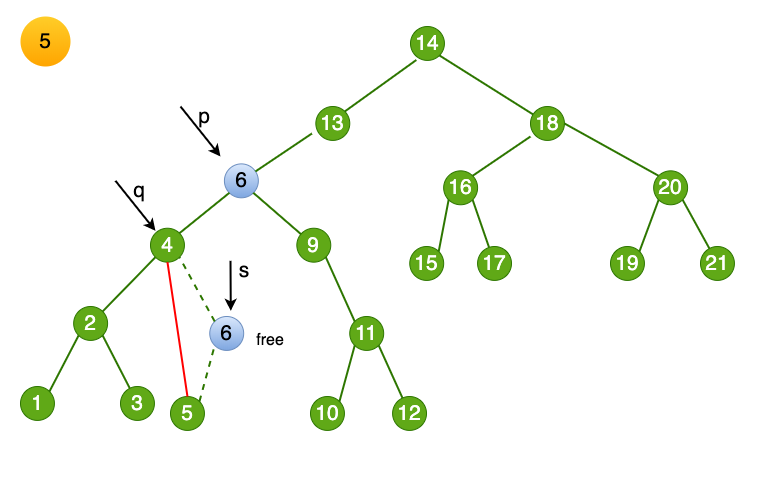
• 最后一步，free 掉删除的目标结点

  

3.2.5 总结

二叉排序树是以连接的方式存储，保持了链式存储结构在执行插入和删除操作时不用移动元素的优点，只要找到合适的插入和删除位置后，仅需修改链接指针即可。