【数据结构与算法】-（2）线性表基础

【数据结构与算法】-（1）基础篇

【数据结构与算法】-（2）线性表基础

【数据结构与算法】-（3）循环链表（单向）

【数据结构与算法】-（4）双向链表和双向循环链表

【数据结构与算法】-（5）链表面试题解析

【数据结构与算法】-（6）栈

【数据结构与算法】-（7）队列

零、前言

上文学到了数据结构和算法的一些基础知识，接下来从最基础的概念，线性表说起。

一、线性表的定义和特点

1.1 定义

定义：零个或多个数据元素的有限序列

线性表，顾名思义，就是有着和线一样特性的表。比如我们乘坐的火车，通常是由许多节车厢组成，车厢首尾相连，最终形成一辆火车。这样的结构，就可以成为线性表。

1.2 线性表的抽象数据类型

线性表的抽象类型定义如下：

ADT 线性表（List）

Data：线性表的数据对象集合为{a1,a2,......an},每个元素的类型均为DataType. 其中,除了第一个元素a1外,每一个元素有且只有一个直接前驱元素,除了最后一个元素an外,每个元素有且只有一个直接后继元素. 数据元素之间的关系是一对一的关系.

Operation

	InitList(*L) :		初始化操作，建立一个空的线性表L<sub>0</sub>
	ListEmpty(L) :    若线性表已存在，返回`true`; 否则返回`false`
	ClearList(*L):     将线性表清空
	GetElem(L, i, &e): 将线性表L 中的第 i 个位置元素值返回给 e
	LocateElm（L，e）：在线性表L 中查找与给定值 e 相等的元素，如果查找成功，返回该元素在表中序号表示成功；否则，返回 0 表示失败
	ListInsert(*L, i, e): 在线性表L 中第 i 个位置插入新元素e
	ListDelete(*L, i, *e): 删除线性表L 中第 i 个位置元素，并用 e 返回其值
	ListLength(L):    返回线性表L 的元素个数

endADT

1.3 线性表的顺序存储结构

1.3.1 顺序存储定义

先来看看线性表两种物理结构的第一种：顺序存储结构

定义：线性表的顺序存储结构，指的是用一段地址连续的存储单元依次存储线性表的数据元素。

示意图如下：

1.3.2 顺序存储方式

线性表的顺序存储结构，就是在内存中找了个空间，通过展位的方式，把一定内存空间给占了，然后把相同数据类型的数据元素一次存放在这块空地中。既然线性表的每个数据元素类型都相同，所以可以用C 语言的一维数组来实现顺序存储结构。

看看线性表的顺序存储的结构

#define MAXSIZE 20
typedef int ElemType;

typedef struct
{
		ElemType data[MaxSize];
		int length;
}Sqlist;

通过观察可以发现，描述顺序存储结构需要三个属性：

• 存储空间的起始位置：数组data，它的存储位置就是存储空间的存储位置。
• 线性表的最大存储容量：数组长度MaxSize
• 线性表的当前长度: length

1.3.3 数据长度与线性表长度区别

• 数组长度时存放线性表的存储空间的长度，存储分配后这个量一般是不变的。
• 线性表的长度时线性表中数据元素的个数，随着线性表的插入和删除操作的进行，这个量是变化的。
• 在任意时刻，线性表的长度应该小于等于数组的长度。

1.4 顺序表的基本操作

1.4.1 顺序表的初始化

Status InitList(Sqlist *L){
    //为顺序表分配一个大小为MAXSIZE 的数组空间
    L->data =  malloc(sizeof(ElemType) * MAXSIZE);
    //存储分配失败退出
    if(!L->data) exit(ERROR);
    //空表长度为0
    L->length = 0;
    return OK;
}

1.4.2 顺序表的插入

/*
 初始条件：顺序线性表L已存在,1≤i≤ListLength(L);
 操作结果：在L中第i个位置之前插入新的数据元素e，L的长度加1
 */
Status ListInsert(Sqlist *L,int i,ElemType e){
    
    //i值不合法判断
    if((i<1) || (i>L->length+1)) return ERROR;
    //存储空间已满
    if(L->length == MAXSIZE) return ERROR;
 
    //插入数据不在表尾,则先移动出空余位置
    if(i <= L->length){
        for(int j = L->length-1; j>=i-1;j--){
       
            //插入位置以及之后的位置后移动1位
            L->data[j+1] = L->data[j];
        }
    }
    
    //将新元素e 放入第i个位置上
    L->data[i-1] = e;
    //长度+1;
    ++L->length;
    
    return OK;
    
}

1.4.3 顺序表的取值

Status GetElem(Sqlist L,int i, ElemType *e){
    //判断i值是否合理, 若不合理,返回ERROR
    if(i<1 || i > L.length) return  ERROR;
    //data[i-1]单元存储第i个数据元素.
    *e = L.data[i-1];
    
    return OK;
}

1.4.3 顺序表的删除

/*
 初始条件：顺序线性表L已存在，1≤i≤ListLength(L)
 操作结果: 删除L的第i个数据元素,L的长度减1
 */
Status ListDelete(Sqlist *L,int i){
    
    //线性表为空
    if(L->length == 0) return ERROR;
    
    //i值不合法判断
    if((i<1) || (i>L->length+1)) return ERROR;
    
    for(int j = i; j < L->length;j++){
        //被删除元素之后的元素向前移动
        L->data[j-1] = L->data[j];
    }
    //表长度-1;
    L->length --;
    
    return OK;
    
}

1.4.5 清空顺序表

/* 初始条件：顺序线性表L已存在。操作结果：将L重置为空表 */
Status ClearList(Sqlist *L)
{
    L->length=0;
    return OK;
}

1.4.6 判断顺序表清空

/* 初始条件：顺序线性表L已存在。操作结果：若L为空表，则返回TRUE，否则返回FALSE */
Status ListEmpty(Sqlist L)
{
    if(L.length==0)
        return TRUE;
    else
        return FALSE;
}

1.4.7 获取顺序表长度

/* ListEmpty元素个数 */
int ListLength(Sqlist L)
{
    return L.length;
}

1.4.8 顺序输出List

/* 初始条件：顺序线性表L已存在 */
/* 操作结果：依次对L的每个数据元素输出 */
Status TraverseList(Sqlist L)
{
    int i;
    for(i=0;i<L.length;i++)
        printf("%d\n",L.data[i]);
    printf("\n");
    return OK;
}

1.4.9 顺序表查找元素并返回位置

/* 初始条件：顺序线性表L已存在 */
/* 操作结果：返回L中第1个与e满足关系的数据元素的位序。 */
/* 若这样的数据元素不存在，则返回值为0 */
int LocateElem(Sqlist L,ElemType e)
{
    int i;
    if (L.length==0) return 0;
    
    for(i=0;i<L.length;i++)
    {
        if (L.data[i]==e)
            break;
    }
  
    if(i>=L.length) return 0;
    return i+1;
}

1.5 顺序存储结构表的优缺点

• 优点
  • 无须为表示表中元素之间的逻辑关系而增加额外的存储空间
  • 可以快速地存取表中任意位置的元素
• 缺点
  • 插入和删除操作需要移动大量元素
  • 当线性表长度变化较大时，难以确定存储空间的容量
  • 造成存储空间的“碎片”

1.5 线性表的链式存储结构

1.5.1 定义

上文提到，顺序存储结构哦的线性表，最大的特点就是插入和删除时，需要移动大量元素，这显然需要耗费时间。

线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素，这组存储单元可以是连续的，也可以是不连续的。这就意味着，这些数据元素可以存在内存未被占用的人一位置。

以前在顺序结构中，每个数据元素只要存数据元素信息就可以了。现在链式结构中，除了要存数据元素信息外，还要存储它的后继元素的存储地址。

• 我们把存储数据元素信息的域成为数据域。

• 把存储直接后继位置的域称为指针域。

• 指针域中存储的信息称做指针或链，这两部分信息组成数据元素的存储映像，称为结点（Node）

• n个结点链接成一个链表，成为线性表的链式存储结构，因为此链表的每个节点中只包含一个指针域，所以叫单链表。

• 链表中第一个结点的存储位置叫做头指针。

• 单链表的第一个结点前附设一个结点，称为头结点。

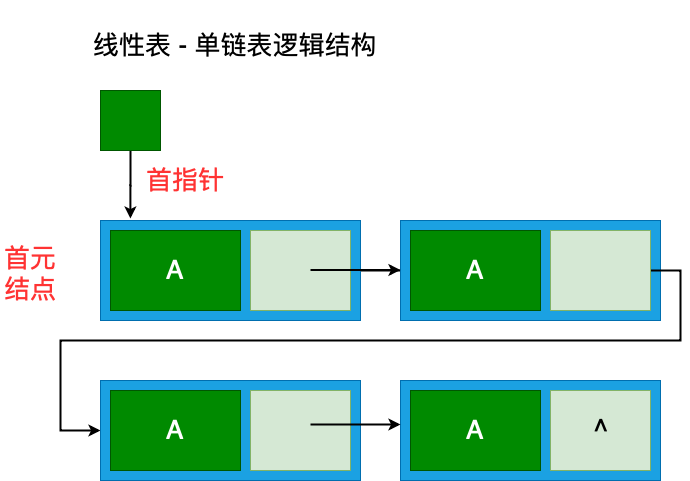
而单链表的逻辑结构如下:

1.5.2 头指针与头结点的异同

头指针	头结点
头指针是指链表指向第一个结点的指针，若链表有头结点，则是指向头结点的指针	头结点是为了操作的统一和方便设立的，放在第一元素的结点之前，其数据域一般无意义（也可存放链表的长度）
头指针具有标示作用，所以常用头指针冠以链表的名字	有了头结点，对在第一元素结点前插入结点和删除第一结点，其操作与其他结点的操作就统一了
无论链表是否为空，头指针均不为空。头指针式链表的必要元素	头结点不一定是链表必须要素

1.5.3 为什么要添加头结点

• 便于首元结点处理
• 便于空表和非空表的统一处理

1.6 单链表

1.6.1 单链表取值

//2.3 单链表取值
/*
 初始条件: 顺序线性表L已存在,1≤i≤ListLength(L);
 操作结果：用e返回L中第i个数据元素的值
 */
Status GetElem(LinkList L,int i,ElemType *e){
    
    //j: 计数.
    int j;
    //声明结点p;
    LinkList p;
    
    //将结点p 指向链表L的第一个结点;
    p = L->next;
    //j计算=1;
    j = 1;
    
    
    //p不为空,且计算j不等于i,则循环继续
    while (p && j<i) {
        
        //p指向下一个结点
        p = p->next;
        ++j;
    }
    
    //如果p为空或者j>i,则返回error
    if(!p || j > i) return ERROR;
    
    //e = p所指的结点的data
    *e = p->data;
    return OK;
    
    
}

1.6.2 单链表的插入

单链表的插入操作，分为两种：

1.6.2.1 前插法

将新结点插入在链表头结点前面，成为前插法

/* 随机产生n个元素值,建立带表头结点的单链线性表L(前插法)*/
void CreateListHead(LinkList *L, int n){
    
    LinkList p;
    
    //建立1个带头结点的单链表
    *L = (LinkList)malloc(sizeof(Node));
    (*L)->next = NULL;
    
    //循环前插入随机数据
    for(int i = 0; i < n;i++)
    {
        //生成新结点
        p = (LinkList)malloc(sizeof(Node));
       
        //i赋值给新结点的data
        p->data = i;
        //p->next = 头结点的L->next
        p->next = (*L)->next;
        
        //将结点P插入到头结点之后;
        (*L)->next = p;
        
    }
}

//3.1 前插法整理创建链表L
iStatus = ClearList(&L);
CreateListHead(&L, 20);
printf("整理创建L的元素(前插法):\n");
ListTraverse(L);

1.6.2.2 后插法

将新结点插入在链表的尾结点后面，称为后插法

/* 随机产生n个元素值,建立带表头结点的单链线性表L(后插法)*/
void CreateListTail(LinkList *L, int n){
    
    LinkList p,r;
 
    //建立1个带头结点的单链表
    *L = (LinkList)malloc(sizeof(Node));
    //r指向尾部的结点
    r = *L;
    
    for (int i=0; i<n; i++) {
        
        //生成新结点
        p = (Node *)malloc(sizeof(Node));
        p->data = i;
        
        //将表尾终端结点的指针指向新结点
        r->next = p;
        //将当前的新结点定义为表尾终端结点
        r = p;
    }
    
    //将尾指针的next = null
    r->next = NULL;
    
}

//3.2 后插法整理创建链表L
iStatus = ClearList(&L);
CreateListTail(&L, 20);
printf("整理创建L的元素(后插法):\n");
ListTraverse(L);

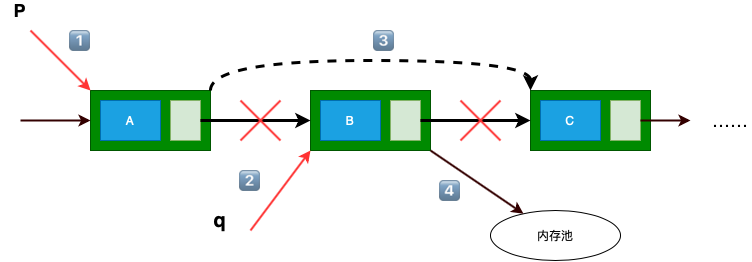
1.6.3 单链表的删除

要删除单链表中指定元素，通插入元素一样，应该先找到该位置的钱去结点。

用C代码实现如下：

//2.4 单链表删除元素
/*
 初始条件：顺序线性表L已存在，1≤i≤ListLength(L)
 操作结果：删除L的第i个数据元素，并用e返回其值，L的长度减1
 */

Status ListDelete(LinkList *L,int i,ElemType *e){
    
    int j;
    LinkList p,q;
    p = (*L)->next;
    j = 1;
    
    //查找第i-1个结点,p指向该结点
    while (p->next && j<(i-1)) {
        p = p->next;
        ++j;
    }
    
    //当i>n 或者 i<1 时,删除位置不合理
    if (!(p->next) || (j>i-1)) return  ERROR;
    
    //q指向要删除的结点
    q = p->next;
    //将q的后继赋值给p的后继
    p->next = q->next;
    //将q结点中的数据给e
    *e = q->data;
    //让系统回收此结点,释放内存;
    free(q);
    
    return OK;
}