【数据结构与算法】-（6）栈

【数据结构与算法】-（1）基础篇

【数据结构与算法】-（2）线性表基础

【数据结构与算法】-（3）循环链表（单向）

【数据结构与算法】-（4）双向链表和双向循环链表

【数据结构与算法】-（5）链表面试题解析

【数据结构与算法】-（6）栈

【数据结构与算法】-（7）队列

1. 概念

1.1 定义

栈 (stack) 是限定仅在表尾进行插入和删除操作的线性表

• 栈的插入操作（push），叫作进栈、入栈。类似子弹入弹夹。
• 栈的删除操作（pop），叫作出栈，也有的叫做弹栈。
• 允许插入和删除的一段叫作栈顶 (top)，另一段底叫作栈底(bottom/rear)

1.2 示意图

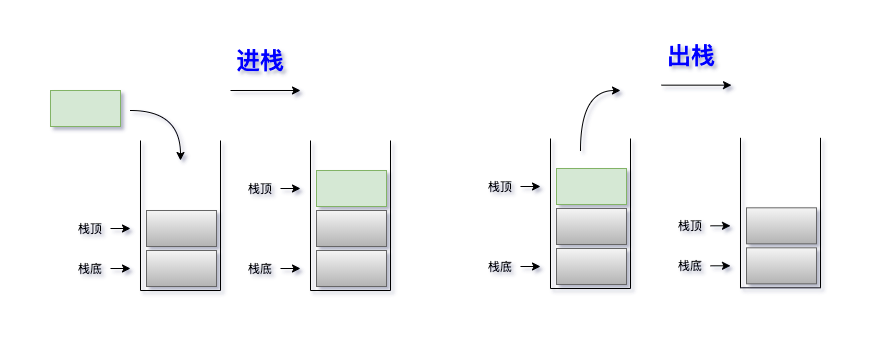
1.2 栈的顺序存储结构及实现

1.2.1 顺序栈结构

顺序栈由一个数据数组和栈顶指针组成：

typedef struct
{
    SElemType data[MAXSIZE];
    int top; /* 用于栈顶指针 */
}SqStack;

和链式结构类似，指针top 永远指向下一个栈内元素。

1.2.2 创建空栈

初始化栈，只需要将栈顶top 处于-1 即可，类似数组，有心数据进来就从0开始排列

Status InitStack(SqStack *S){
   
    S->top = -1;
    return OK;
}

1.2.3 清空一个栈

清空栈也栈顶top 处于-1 即可。

Status ClearStack(SqStack *S){
    // 只需要修改top标签 -1.
    S->top = -1;
    return OK;
}

1.2.4 判断栈是否为空

由于栈内只要有有元素，栈顶top都会移动位置，所以只需要判断是否在-1 即可

Status StackEmpty(SqStack S){
    return S.top == -1;
}

1.2.5 返回栈的长度

由于栈顶从0开始排列起来，长度必须上top的序号+1

int StackLength(SqStack S){
    return S.top + 1;
}

1.2.6 获取栈顶元素

类似数组一样，栈定元素为最后一个元素，即S.data[S.top]

Status GetTop(SqStack S,SElemType *e){
    if (S.top == -1)
        return ERROR;
    else
        *e = S.data[S.top];
   
    return OK;
}

1.2.7 插入元素e 为新栈顶元素（压栈）

压栈即把top 序号 位置提升1位，top位的元素为新元素。

Status PushData(SqStack *S, SElemType e){
    
    //栈已满
    if (S->top == MAXSIZE -1) {
        return ERROR;
    }
    
    //栈顶指针+1;
    S->top ++;
    //将新插入的元素赋值给栈顶空间
    S->data[S->top] = e;
    
    return OK;
}

1.2.8 删除栈定元素，并用e带回（出栈）

出栈与入栈恰恰相反，将top 位的元素弹出，同时将top 序号减1

Status Pop(SqStack *S,SElemType *e){
    //空栈,则返回error;
    if (S->top == -1) {
        return ERROR;
    }
    //将要删除的栈顶元素赋值给e
    *e = S->data[S->top];
    //栈顶指针--;
    S->top--;
    
    return OK;
}

1.2.9 从栈底到栈顶每个元素打印（遍历）

Status StackTraverse(SqStack S){
    int i = 0;
    printf("此栈中所有元素");
    while (i<=S.top) {
        printf("%d ",S.data[i++]);
    }
    printf("\n");
    return OK;
}

1.3 栈的链式存储结构及实现

1.3.1 示意图

栈道链式存储结构，简称链栈。

链栈的示意图和顺序结构很类似，如图所示了入栈和出栈的流程：

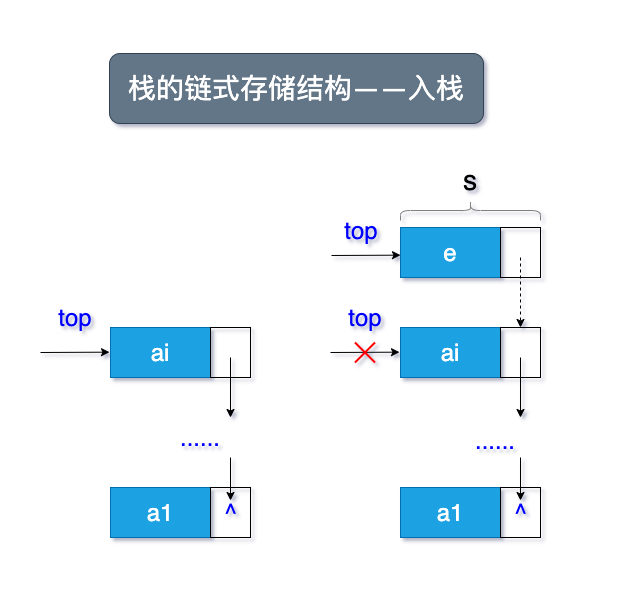
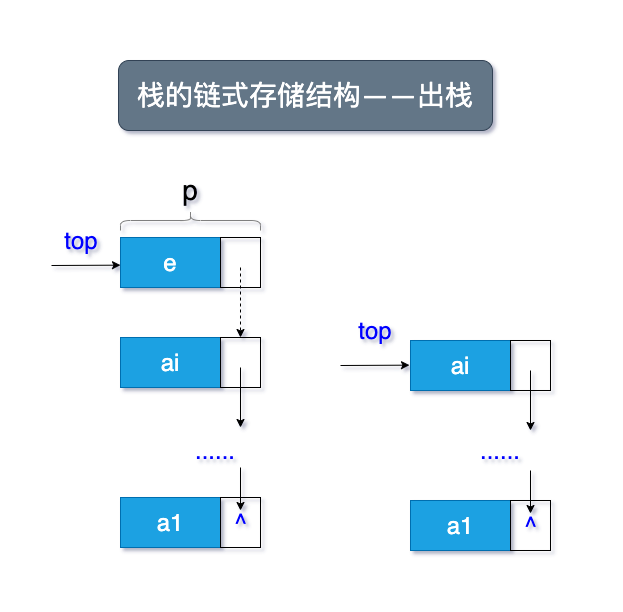
1.3.2 链栈结构

链栈道结构和单链表很相似：

• 节点的结构如下：

  typedef struct StackNode
  {
      SElemType data;
      struct StackNode *next;
  }StackNode,*LinkStackPtr;

• 链栈结构如下：

  typedef struct
  {
      LinkStackPtr top;
      int count;
  }LinkStack;

1.3.3 创建空栈

Status InitStack(LinkStack *S)
{
    S->top=NULL;
    S->count=0;
    return OK;
}

1.3.4 清空一个栈

Status ClearStack(LinkStack *S){
    LinkStackPtr p,q;
    p = S->top;
    while (p) {
        q = p;
        p = p->next;
        free(q);
    }
    S->count = 0;
    return OK;
    
}

1.3.5 判断栈是否为空

Status StackEmpty(LinkStack S){
    return S.count == 0;
}

1.3.6 返回栈的长度

int StackLength(LinkStack S){
    return S.count;
}

1.3.7 获取栈顶元素

Status GetTop(LinkStack S,SElemType *e){
    if(S.top == NULL)
        return ERROR;
    else
        *e = S.top->data;
    return OK;
}

1.3.8 插入元素e 为新栈顶元素（压栈）

Status Push(LinkStack *S, SElemType e){
    
    //创建新结点temp
    LinkStackPtr temp = (LinkStackPtr)malloc(sizeof(StackNode));
    //赋值
    temp->data = e;
    //把当前的栈顶元素赋值给新结点的直接后继, 参考图例第①步骤;
    temp->next = S->top;
    //将新结点temp 赋值给栈顶指针,参考图例第②步骤;
    S->top = temp;
    S->count++;
    return OK;
}

1.3.9 删除栈定元素，并用e带回（出栈）

Status Pop(LinkStack *S,SElemType *e){
    LinkStackPtr p;
    if (StackEmpty(*S)) {
        return ERROR;
    }
    //将栈顶元素赋值给*e
    *e = S->top->data;
    //将栈顶结点赋值给p,参考图例①
    p = S->top;
    //使得栈顶指针下移一位, 指向后一结点. 参考图例②
    S->top= S->top->next;
    //释放p
    free(p);
    //个数--
    S->count--;
    return OK;
}

1.3.10 从栈底到栈顶每个元素打印（遍历）

Status StackTraverse(LinkStack S){
    LinkStackPtr p;
    p = S.top;
    while (p) {
        printf("%d ",p->data);
        p = p->next;
    }
    printf("\n");
    return OK;
}

1.4 栈与递归

1.4.1 递归的定义

直接调用自己或通过一系列的调用语句间接地调用自己的函数，叫做递归函数。

1.4.2 递归的特点

每个递归定义必须有一个条件，满足时递归不再进行，即不再引用自身而是返回值退出。

1.4.3 递归与迭代的区别

• 迭代： 使用的是循环结构。
• 递归：使用的是选择结构。是程序结构更清晰、更简洁、更容易让人理解，从而减少读懂代码的时间。

1.4.4 递归的使用场景

• 定义是递归的
• 数据结构是递归的
• 问题的解法是递归的

1.4.5 递归应用——斐波那契数列

问题：如果兔子2个月之后就会有繁殖能力，那么一对兔子每个月能生出一对兔子；假设所有的兔子都不死，那么n个月后能生出多杀只兔子呢？

解法：

int Fbi(int i){
    if(i<2)
        return i == 0?0:1;
    return Fbi(i-1)+Fbi(i-2);
}

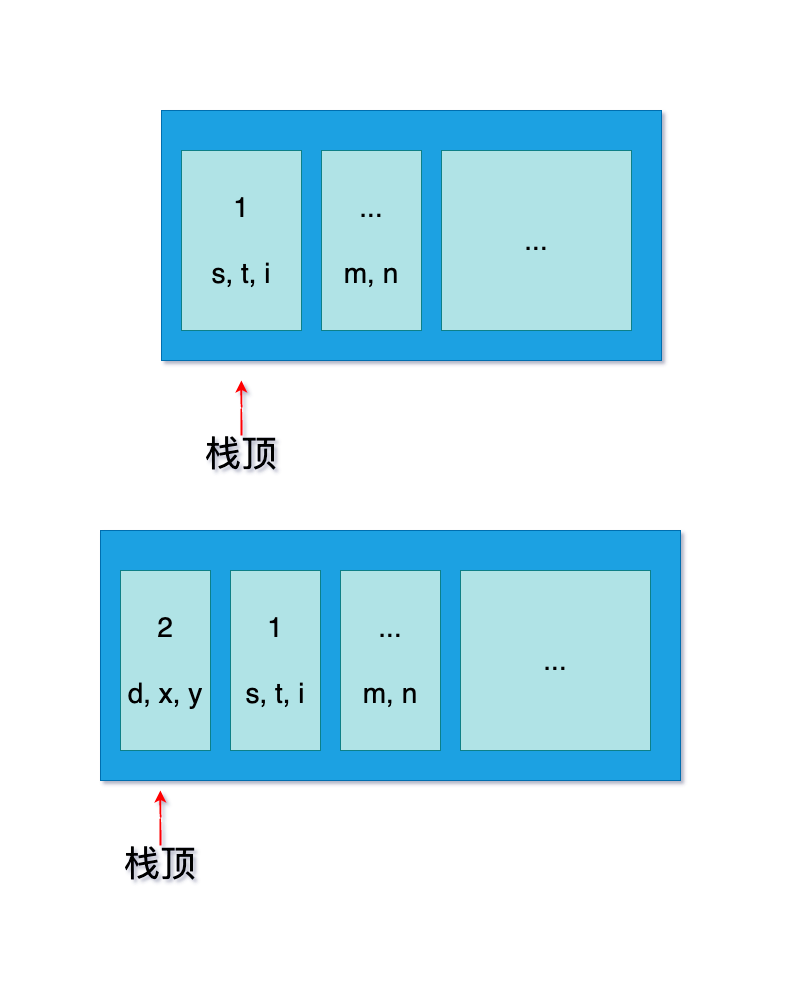
1.4.6 递归过程与递归工作栈

我们日常使用函数时，常有函数内套用其他函数，而其他函数又会套用其他的函数，比如如下的代码：

void main(){
  	int m, n;
  	first(m, n);
} 

int first(int s, int t){
  	int i;
  	//...
  	second(i);
}

int second(int d){
  	int x,y;
  	// blablabla
}

这样的结构，其实也是递归的应用，这种应用叫做递归工作站，其结构示意图如下: