【数据结构与算法】-（5）链表面试题解析

【数据结构与算法】-（1）基础篇

【数据结构与算法】-（2）线性表基础

【数据结构与算法】-（3）循环链表（单向）

【数据结构与算法】-（4）双向链表和双向循环链表

【数据结构与算法】-（5）链表面试题解析

【数据结构与算法】-（6）栈

【数据结构与算法】-（7）队列

序言

之前复习了一下数据结构以及线性表的基础，继续来做一些习题，巩固一下。

Q1 链表合并

1. 题目：

将两个递增的有序链表合并为一个有序链表；要求结果链表仍然是用两个链表的存储空间，不另外占用其他的存储空间；表中不允许有重复的数据

如La{1 ,2, 3}, Lb{3, 6, 9}, 合并成为 Lc{1, 2, 3, 6, 9}

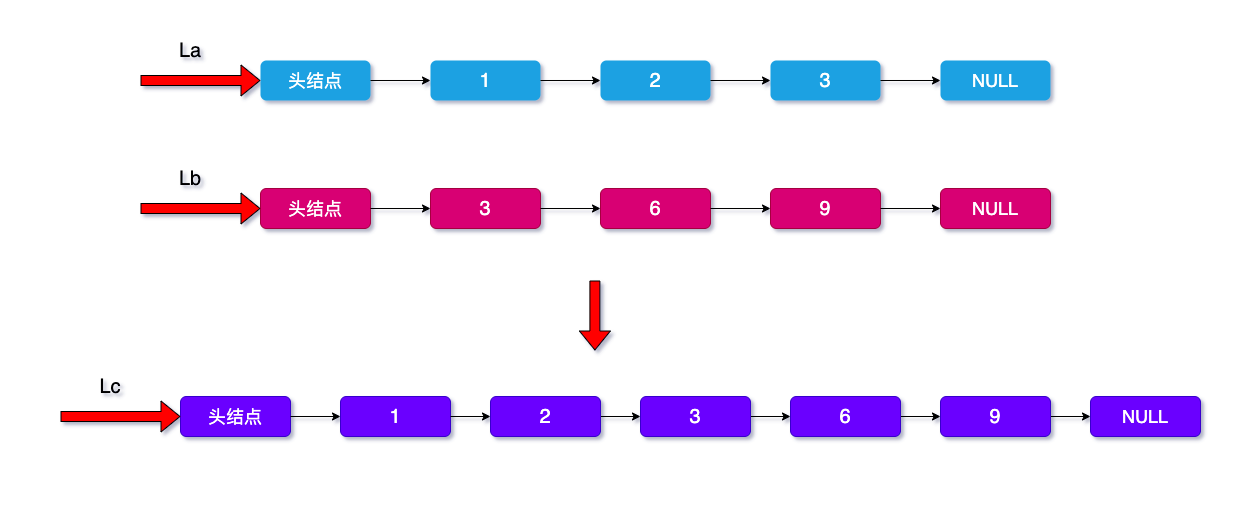
2. 分析：

本题要求如下：

• 两个都是递增有序链表
• 不允许重复数据
• 结果要求保持递增关系，可以考虑后插法
• 不占用额外空间，也不允许新建维持逻辑

3. 算法思路：

1. 准备临时变量：头指针Lc——由于要求不占用额外空间，Lc指向（借用）La 的头结点
2. 依次循环La、Lb ，
   1. 比较pa、pb两者的 data 值大小，取较小者存到Lc里
   2. 比较较小者剩余链表，与较大者的data，循环往复

4. 代码实现：

ListNode* mergeTwoLists(ListNode* La, ListNode* Lb) {
       if(La == NULL)
            return Lb;
        else if(Lb == NULL)
            return La;

        ListNode *Lc = NULL;
        if(La-> data < Lb-> data){
            Lc = La;
            Lc->next = mergeTwoLists(La->next, Lb);

        }else{
            Lc = Lb;
            Lc->next = mergeTwoLists(La, Lb->next);
        }
        return Lc;
}

5. 流程图解

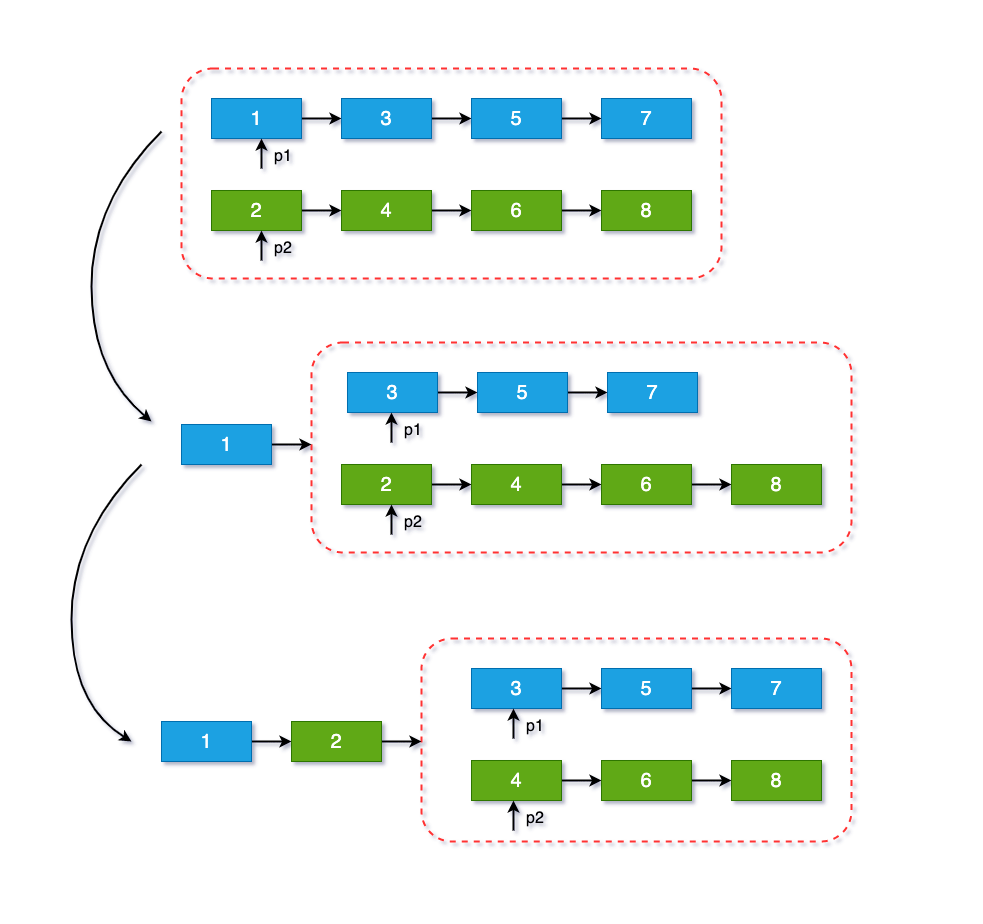
Q2 链表：求重

1. 题目：

已知两个链表A和B分别表示两个集合.其元素递增排列. 设计一个算法,用于求出A与B的交集,并存储在A链表中;

例如:

La = {2,4,6,8}; Lb = {4,6,8,10};

Lc = {4,6,8}

2. 分析：

• 需要比较相同元素，予以保留
• 比较后不同的元素，予以删除

3. 算法思路

这道题目与上道题恰恰相反，在依次循环后，留下相同的元素。

1. 准备临时变量：
   1. 原始链表La、Lb、
   2. 链表 La 和 Lb 各自的首元结点指针pa、 pb、
   3. 头指针Lc——由于要求不占用额外空间，Lc指向（借用）La 的头结点
2. 依次循环La、Lb ，
   1. 比较pa、pb两者的 data 值大小
   2. 若相等，把pa存到Lc里，释放pb指定结点
   3. 若不相等，释放掉较小的元素
3. 若循环至某一方为空，删除/释放非空表所有元素

4. 代码实现

void Intersection(LinkList *La, LinkList *Lb, LinkList *Lc){
    //目标: 求2个递增的有序链表La,Lb的交集, 使用头指针Lc指向带回;
    LinkList pa,pb,pc,temp;
    //pa 是链表La的工作指针,pb 是链表Lb的工作指针, 初始化为首元结点;La的头结点作为Lc的头结点;
    pa = (*La)->next;
    pb = (*Lb)->next;
    *Lc = pc = *La;

    while (pa && pb) {

        if (pa->data == pb->data) {
            //相等,交集并入结果链表中;
            //(1).取La中的元素,将pa链接到pc的后面,pa指针后移;
            pc->next = pa;
            pc = pa;
            pa = pa->next;
            //(2)删除Lb中对应相等的元素
            temp = pb;
            pb = pb->next;
            free(temp);
        }else if(pa->data < pb->data){

            //删除较小值La的元素;
            temp = pa;
            pa = pa->next;
            free(temp);
        }else{
            //删除较小值Lb中的元素
            temp = pb;
            pb = pb->next;
            free(temp);
        }
    }

    //Lb为空,删除非空表La中的所有元素
    while (pa) {

        temp = pa;
        pa = pa->next;
        free(temp);
    }

    //La为空,删除非空表Lb中的所有元素
    while (pb) {
        temp = pb;
        pb = pb->next;
        free(temp);
    }


    pc->next = NULL;
    free(*Lb);
}

5. 流程图解

Q3 链表原地旋转【面试常有】

1. 题目：

设计一个算法,将链表中所有节点的链接方向”原地旋转”，即要求仅仅利用原表的存储空间。换句话说,要求算法空间复杂度为O(1);

例如:L = {0,2,4,6,8,10}, 逆转后: L = {10,8,6,4,2,0};

2. 分析：

• 不可以开辟空间
• 只能移动指针
• 首选头插法

3. 算法思路：

1. 保持当前头结点的下个结点
2. 将当前头结点的指向指到上一个结点
3. 把当前头结点保存为上一个结点
4. 将头结点的下一个结点，设定为头结点

4. 代码实现：

struct LinkList* reverseList(struct LinkList* head){
    if(head == NULL || head->next == NULL)
        return head;

    struct LinkList *preNode = reverseList(head->next);

    head->next->next = head;
    head->next = NULL;

    return preNode;

}

5. 流程图解

Q4 链表删除指定元素

1. 题目：

设计一个算法，删除递增有序链表中值大于等于mink且小于等于maxk（mink, maxk是给定的两个参数,其值可以和表中的元素相同,也可以不同）的所有元素;

2. 分析：

• 链表递增
• 给定上边界、下边界
• 上下边界找到后，桥接起来
• 边界中其他元素删除

3. 算法思路：

1. mink：循环链表1次，找到第一个大于mink的结点，记住其前驱结点pre
2. maxk：循环链表2次，找到大于等于maxk 的结点，用p标记
3. 桥接：把 pre -> next 指向结点p
4. 循环释放，释放pre、p 中间的结点

4. 代码实现：

void DeleteMinMax(LinkList *L, int mink, int maxk){
    //目标: 删除递增有序链表L中值大于等于mink 和小于等于maxk的所有元素

    LinkList p,q,pre;
    pre = *L;
    LinkList temp;

    //p指向首元结点
    p = (*L)->next;

    //1.查找第一值大于mink的结点
    while (p && p->data < mink) {
        //指向前驱结点
        pre = p;
        p = p->next;
    }

    //2.查找第一个值大于等于maxk的结点
    while (p && p->data<=maxk) {
        p = p->next;
    }

    //3.修改待删除的结点指针
    q = pre->next;
    pre->next = p;

    while (q != p) {
        temp = q->next;
        free(q);
        q = temp;
    }
}

5. 流程图解

Q5 数组平移

1. 题目：

设将n(n>1)个整数存放到一维数组R中, 试设计一个在时间和空间两方面都尽可能高效的算法;将R中保存的序列循环左移p个位置 (0<p<n) 个位置， 即将R中的数据由 (x0,x1,……,xn-1) 变换为(xp,xp+1,…,xn-1,x0,x1,…,xp-1).

例如:

pre[10] = {0,1,2,3,4,5,6,7,8,9},

n = 10,p = 3;

pre[10] = {3,4,5,6,7,8,9,0,1,2}

2. 分析：

• 数组而非链表
• 往左移动，原左边的元素依次推到右边
• 本质上两个区块元素交换，可考虑先原地旋转
• 再将两个区块元素各自原地旋转

3. 算法思路：

1. 将原数组原地旋转，成为[9, 8, 7, 6, 5, 4, 3, 2, 1, 0]
2. 从后面第p位，将原数组断成为[9, 8, 7, 6, 5, 4, 3], [2, 1, 0]
3. 再将新的两个数组原地旋转[3, 4, 5, 6, 7, 8, 9], [0, 1, 2]
4. 合并成为目标数组 [3, 4, 5, 6, 7, 8, 9, 0, 1, 2]

4. 代码实现：

void Reverse(int *pre,int left ,int right){

    //将数组R中的数据原地逆置

    //i等于左边界left,j等于右边界right;
    int i = left,j = right;
    int temp;

    //交换pre[i] 和 pre[j] 的值
    while (i < j) {

        //交换
        temp = pre[i];
        pre[i] = pre[j];
        pre[j] = temp;

        //i右移,j左移
        i++;
        j--;
    }
}

void LeftShift(int *pre,int n,int p){

    //将长度为n的数组pre 中的数据循环左移p个位置
    if (p>0 && p<n) {
        //1. 将数组中所有元素全部逆置
        Reverse(pre, 0, n-1);
        //2. 将前n-p个数据逆置
        Reverse(pre, 0, n-p-1);
        //3. 将后p个数据逆置
        Reverse(pre, n-p, n-1);

    }
}

5. 流程图解

Q6 链表查主元素

1. 题目：

已知一个整数序列A = (a0,a1,a2,…an-1)，其中(0<= ai <=n),(0<= i<=n)。

若存在ap1= ap2 = …= apm = x，且m>n/2(0<=pk<n,1<=k<=m)，则称x 为 A的主元素。

例如,A = (0,5,5,3,5,7,5,5)，则5是主元素；若B = (0,5,5,3,5,1,5,7)，则A 中没有主元素，假设A中的n个元素保存在一个一维数组中，请设计一个尽可能高效的算法,找出数组元素中的主元素，若存在主元素则输出该元素，否则输出-1.

2. 分析：

• 递增数组
• 数组中可能有多次出现的元素
• 出现次数超过一半 > n/2 ，即为目标元素

3. 算法思路：

1. 假定一个候选主元素 key
2. 依次遍历循环数组，将key 与数组元素对比，记录其与其他元素相同的次数，记作count，count 初始值为1
3. 如果遇到相同元素，count++ ，否则 count++
4. 循环中，如遇到count 为0，即重复次数达不到一半，将遇到的下一个元素设定为key, count 置1， 重新循环
5. 再次循环数组，计算数组中元素与key 重合次数，如大于 n/2， 即为主元素，否则无主元素。

4. 代码实现：

int MainElement(int *A, int n){

    //目标: 求整数序列A中的主元素;
    //count 用来计数
    int count = 1;
    //key 用来保存候选主元素, 初始A[0]
    int key = A[0];

    //(1) 扫描数组,选取候选主元素
    for (int i = 1; i < n; i++) {

        //(2) 如果A[i]元素值 == key ,则候选主元素计数加1;
        if (A[i] == key) {
            count++;
        }else{
            //(3) 当前元素A[i] 非候选主元素,计数减1;
            if(count >0){
                count--;

            }else{
               //(4) 如果count 等于0,则更换候选主元素,重新计数
                key = A[i];
                count = 1;
            }

        }
    }
    //如果count >0
    if (count >0){
        //(5)统计候选主元素的实际出现次数
        for (int i = count = 0; i < n; i++)
            if (A[i] == key) count++;
    }

    //(6)判断count>n/2, 确认key是不是主元素
    if (count > n/2) return key;
    else return -1; //不存在主元素

}

Q7 链表的元素删除

1. 题目

用单链表保存m个整数, 结点的结构为(data,link),且|data|<=n(n为正整数)。

现在要去设计一个时间复杂度尽可能高效的算法。对于链表中的data 绝对值相等的结点, 仅保留第一次出现的结点,而删除其余绝对值相等的结点。例如,链表A = {21,-15,15,-7,15}, 删除后的链表 A = {21,-15,-7};

2. 分析：

• 时间复杂度高效
• 可用空间换时间——即开辟更多空间
• 循环原链表，若元素已经出现过，保存第一个，删除其他绝对值相等的元素

3. 算法思路：

1. 可额外开辟大小为 n + 1 的辅助数组，初始值为 0
2. 从首元结点开始遍历链表，检查元素值，用t[|data|] 计算链表元素出现的次数：
   1. 若元素[｜data｜] 为0，即首次出现，保留结点，使得 t[|data|] = 1
   2. 若 [|data|] 不为 0， 则将该结点从链表中删除。

x

void DeleteEqualNode(LinkList *L,int n){

    //目标: 删除单链表中绝对值相等的结点;
    //1. 开辟辅助数组p.
    int *p = alloca(sizeof(int)*n);
    LinkList r = *L;

    //2.数组元素初始值置空
    for (int i = 0; i < n; i++) {
        *(p+i) = 0;
    }

    //3.指针temp 指向首元结点
    LinkList temp = (*L)->next;

    //4.遍历链表,直到temp = NULL;
    while (temp!= NULL) {

        //5.如果该绝对值已经在结点上出现过,则删除该结点
        if (p[abs(temp->data)] == 1) {

            //临时指针指向temp->next
            r->next = temp->next;
            //删除temp指向的结点
            free(temp);
            //temp 指向删除结点下一个结点
            temp = r->next;
        }else
        {
            //6. 未出现过的结点,则将数组中对应位置置为1;
            p[abs(temp->data)] = 1;
            r = temp;
            //继续向后遍历结点
            temp = temp->next;
        }
    }

}

5. 复杂度

• 时间复杂度: O(m), 对长度为m的链表进行一趟遍历,则算法时间复杂度为O(m);
• 空间复杂度: O(n)