【数据结构与算法】-（7）队列

算法 数据结构 队列
发布日期:   2020-04-14
文章字数:   2.3k
阅读时长:   10 分
阅读次数:  

【数据结构与算法】-（1）基础篇

【数据结构与算法】-（2）线性表基础

【数据结构与算法】-（3）循环链表（单向）

【数据结构与算法】-（4）双向链表和双向循环链表

【数据结构与算法】-（5）链表面试题解析

【数据结构与算法】-（6）栈

【数据结构与算法】-（7）队列

一、概念

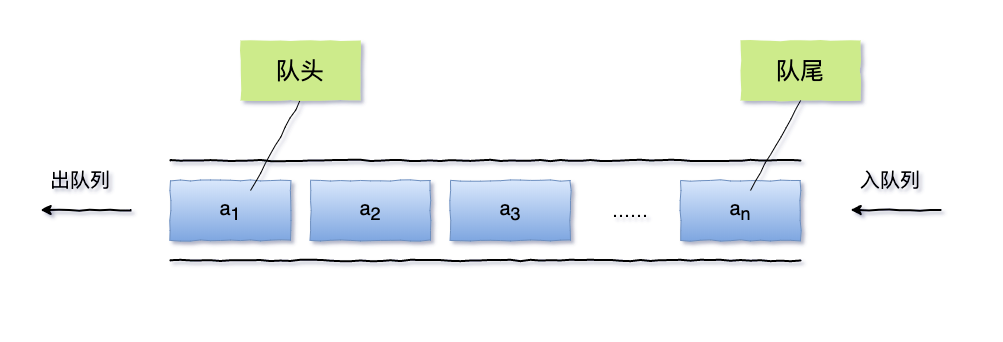
队列 (queue) 是只允许在一端进行插入操作、而在另一端进行删除操作的线性表

队列是一种先进先出（First In First Out）的线性表，简称FIFO。允许插入的一端称为队尾(rear)，允许删除的一端称为队头(front)。

队列结构

二、操作

入队和出队：正如上文提到的，队列讲究的是先进先出的原则。队列的内部规则，好比大学上课时的占座位，先占到座位的总是前三排，来得晚的只能做到后面去了，等到下课了，先出去的也往往是前三排，也就是先来的那些同学。

给队列的进队入队画了个示意图如下：

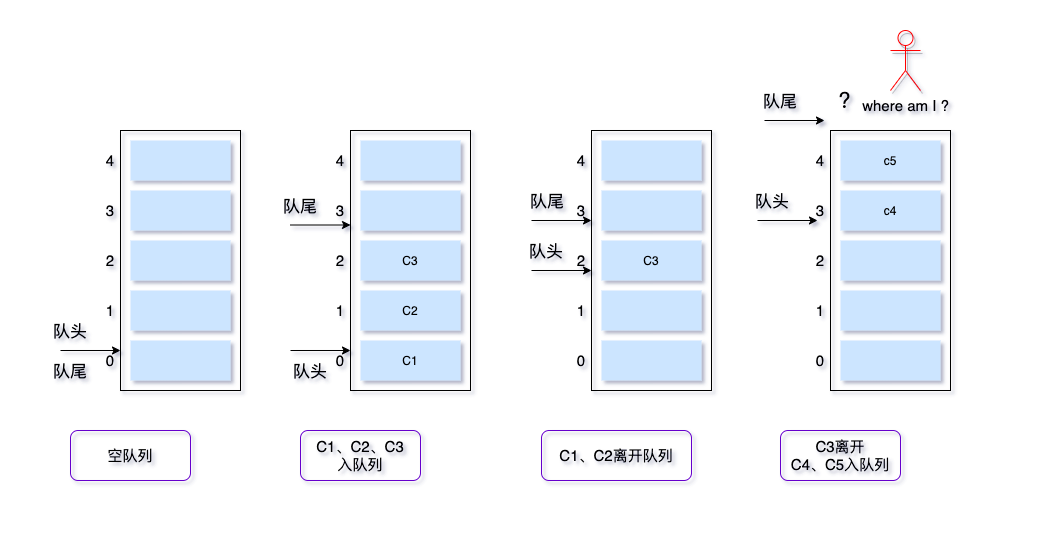
队列的入队出队

三、循环队列

3.1 原理

线性表有顺序存储和链式存储，队列作为线性表的一种，同样有循环队列的结构。

像上图中，当C3离开，相继加入了C4和C5，队尾指针就要指出到队列外了，这时就会报出数组越界的错误，但是可以看到队列下方0、1、2位都是空的，这种情况叫做“假溢出”。

为了解决这种前面空，后面满的情况，我们经常采用解决方案，就是头尾相连的循环。

队列的头尾相连的循环结构称为循环队列

引入循环队列的概念，是为了解决假溢出的现象，那么，究竟什么时候队列真正满了呢？

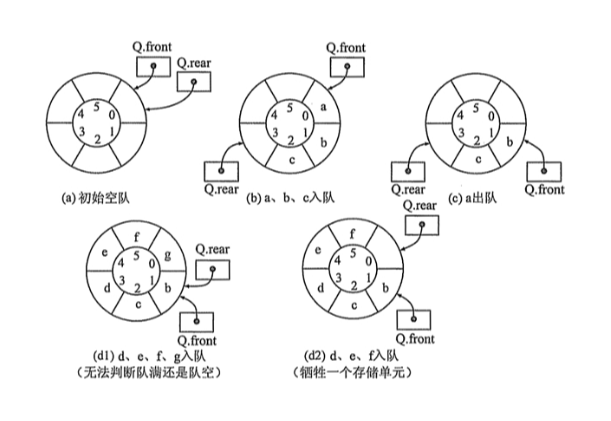
我们根据下图分析：

  • 当初始时，队列空：此时 Q.front = Q.rear
  • 当a、b、c 依次入队，front 不变，rear 指向到元素c后面
  • 当a离开，front 下沉，指向b
  • 当d、e、f、g入队后，此时rear指向最后一个元素b，此时与front重合

此时rear、 front再次重合，回到老路上了？

解决办法是：预留一个元素位，防止重合。

也就是说当队列满时，还会有一个空闲的空间。如最后一张图所示，这样rear和front 不会重合。

所以判断队伍满的条件是：

  • 队列满：Q.front = (Q.rear + 1) % MaxSize

循环队列的入队出队

3.2 顺序存储结构实现

3.2.1 创建队列：

创建队列比较简单，只需要使得rear、front 都为0 即可

  1. 初始化顺序结构的队列结构如下:

    #define MAXSIZE 20

    typedef struct{
        QElemType data[MAXSIZE];
        int front;
        int rear;
    }SqQueue;

  2. 初始化一个空队列

    typedef int Status;
    #define OK      1;

    Status InitQueue(SqQueue *q){
        q->front = q->rear = 0;
        return OK;
    }

3.2.2 清空一个队列：

和创建队列基本相同

Status ClearQueue(SqQueue *q){
    q->front = q->rear = 0;
    return OK;
}

3.2.3 判断是否是空队列：

只需查看rear 和front 是否相等

Status CheckIfEmpty(SqQueue *q){
    return q->front == q->rear ;
}

3.5 返回队列的长度：

需要将尾部减去头部，因为有循环，所以最后要加上MAXSIZE 最后MAXSIZE取模

Status getLength(SqQueue q){
    return (q.rear - q.front + MAXSIZE) % MAXSIZE;
}

3.6 获得队头的元素

#define ERROR   0;

Status getHeadItem(SqQueue q, QElemType e){
    if(q.front == q.rear ) return ERROR;
    e = q.data[q.front];
    return OK;
}

3.7 元素入队

Status EnQueue(SqQueue *q, QElemType e)
{
    // 判断队伍是否满了
    if ((q->rear + 1) % MAXSIZE == q->front)  {
        return ERROR;
    }
    q->data[q->rear] = e;
    q->rear = ( q->rear + 1 ) %MAXSIZE;
    return OK;
}

3.8 元素出队列

Status DeQueue(SqQueue *q, QElemType *e)
{
    // 先判断队伍是否为空
    if (q->rear == q->front) {
        return ERROR;
    }
    *e = q->data[q->front];
    q->front = (q->front + 1 ) % MAXSIZE;

    return OK;
}

3.9 遍历队列中的元素

Status ShowQueue(SqQueue q)
{
    if (q.rear == q.front) {
        return ERROR;
    }
    int i =  q.front;
    while ((i + q.front) != q.rear) {
        printf("%d", q.data[i]);
        i = (i + 1) % MAXSIZE;
    }
    return OK;
}

将以上方法执行的业务代码如下：

int main(int argc, const char * argv[]) {
    // insert code here...

    // 初始化队列
    Status j;
    SqQueue Q;
    QElemType d;
    InitQueue(&Q);
    printf("已经初始化队列");
  
    // 判断是否为空
    printf("队列是否为空呢 %u(1:yes 0:no)", CheckIfEmpty(Q));
    
    // 元素入队列
    printf("开始往队列添加元素\n");
    for (int i = 0; i < 5; i++) {
        EnQueue(&Q, i);
    }
    // 遍历队列
    ShowQueue(Q);
    printf("队列是否为空呢 %u(1:yes 0:no)\n", CheckIfEmpty(Q));
    
    // 获队列的长度
    printf("队列的长度是 %d\n\n", getLength(Q));
    
    // 出队列
    printf("出队\n");
    DeQueue(&Q, &d);
    ShowQueue(Q);
    
    // 获取队列的头
    j = getHeadItem(Q, d);
    if (j) {
        printf("头元素是%d\n" , j);
    }
    
    // 清空队列
    ClearQueue(&Q);
    printf("清空完成，现在队列打印长度为%d\n\n", getLength(Q));
    
    return 0;
}

打印结果如下：

打印结果

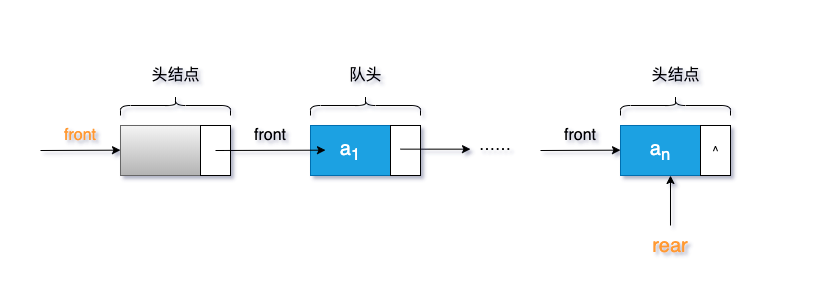
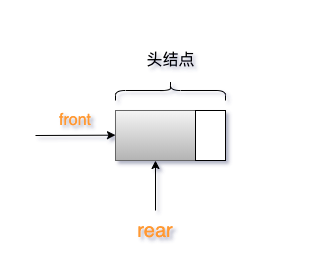
3.3 链式存储结构的实现

链式结构的队列结构图：

链式结构的队列链式结构的空队列

操作实现如下：

3.3.1 链队列结构：

  1. 队列结点结构如下

    typedef int QElemType;

    typedef struct Node {
        QElemType data;
        struct Node * next;
    }Node, *QueuePtr;

  2. 队列结构如下: 只需创建2个指针

    typedef struct {
        QueuePtr front, rear;
    }QueueLinkList;

3.3.2 创建队列

创建链式结构的队列，只需要创建空间、将front 的next 指向空即可

Status createLink(QueueLinkList *q)
{
    q->front = q->rear = (QueuePtr)malloc(sizeof(QueuePtr));
    if (q->front == NULL) {
        return ERROR;
    }
    q->front->next = NULL;
    
    return OK;
}

3.3.3 销毁队列

销毁队列的步骤只需要依次free队列中的元素，这里用q->rear 来临时保管front 指向的元素。

具体操作如下

// 销毁
Status destroyLink(QueueLinkList *q)
{
    while (q->rear) {
        q->rear = q->front->next;
        free(q->front);
        q->front = q->rear;
    }
    return OK;
}

3.3.4 清空一个队列

主要分三步：

  1. 将 rear 指向 front， 即使得首尾相等，名义上成为了空队列
  2. 保留front 的next 元素，断开front 的next
  3. 依次释放队列中元素

来看下代码的实现：

Status clearLink(QueueLinkList *Q)
{
    // 创建2个临时指针变量
    QueuePtr p, q;
    
    // 将尾结点放到头结点
    Q->rear = Q->front ;
    
    // 用q 临时接收 首元结点
    q = Q->front->next;
    
    // 将头结点与后面断开
    Q->front->next = NULL;
    
    // 循环遍历，把接收到Q->front 后面的元素统统释放
    while (q) {
        p = q;
        q = q->next;
        free(p);
    }
    return OK;
}

3.3.5 判断是否为空队列

只需查看rear 和front 是否相等

Status CheckIfEmpty(SqQueue *q){
    return q->front == q->rear ;
}

3.3.6 返回队列的长度

定义一个递增变量，记下循环从 front 到 rear 的次数，即为长度

Status getLength(QueueLinkList Q)
{
    // 定义递增变量 i
    int i = 0 ;

    // 定义一个指针指向 front
    QueuePtr p = Q.front;
    
    // 循环
    while (Q.rear != p) {
        i++;
        p = p->next;
    }
    return i;
}

3.3.7 获取队头的元素

Status getHead(QueueLinkList Q, QElemType e)
{
    if (Q.front == Q.rear) { 
      return ERROR;   
    }
    e  = Q.front->next->data;
    return OK ;
}

3.3.8 元素入队列

入队列的操作和顺序的类似，步骤有以下：

  1. 创建新结点，并确保结果不为空
  2. 将新结点赋值，指向为NULL
  3. 将原链队列的rear 端指向新结点
  4. 将新结点作为原链队列的 rear
Status enQueue(QueueLinkList *Q, QElemType e)
{
    QueuePtr s = (QueuePtr)malloc(sizeof(QueuePtr));
    if (!s) {
        return ERROR;
    }
    
    s->data = e;
    s->next = NULL;
    
    Q->rear->next = s;
    Q->rear = s;
   
    
    return OK;
}

3.3.9 元素出队列

出队列，需要先确认现有队列不为空，以及将现有的front 进行出队列操作

代码实现如下：

Status deueue(QueueLinkList *Q, QElemType *e)
{
    if (Q->rear == Q->front) {
        return ERROR;
    }
    QueuePtr p ;
    p = Q->front->next;
    *e = p->data;
    
    Q->front->next = p->next;
    if (Q->rear == p) {
        Q->rear = Q->front;
    }
    free(p);
    
    return OK ;
}

3.3.10 遍历元素

// 遍历
Status showLink(QueueLinkList Q)
{
    if (Q.rear == Q.front) {
        return ERROR;
    }
    QueuePtr p = Q.front->next;
    while (p ) {
        printf("%d\n", p->data);
        p = p->next;

    }
    return OK;
}

3.3.11 总结业务

业务代码如下:


int main(int argc, const char * argv[]) {

    QueueLinkList Q;
    printf("开始创建\n");
    createLink(&Q);
    printf("创建成果，当前长度      %d\n", getLength(Q));
    printf("依次添加元素\n");

    int i = 1;
    while (i < 10) {
        enQueue(&Q, i);
        i++;
    }
    printf("添加成功，新队列元素为\n");
    showLink(Q);
    
    QElemType head = 0;
    Status j = getHead(Q, head);
    if (j) {
        printf("该队头为%d\n\n",j );
    }
    printf("开始出队\n");
    Status result = deueue(&Q, &head);
    if (result) {
        printf("出队成功，新队列元素为\n");
        showLink(Q);
    }

    // 清空队列
    Status clearResult = clearLink(&Q);
    if (clearResult) {
        printf("清空成功，新队列元素为\n");
        showLink(Q);
    }else{
        printf("清空失败\n");

    }
 
    // 销毁队列
    Status destroyResult = destroyLink(&Q);
    if (destroyResult) {
        printf("销毁成功，新队列元素为\n");
        showLink(Q);
    }else{
        printf("销毁失败\n");

    }

    
    return 0;

}

最终结果如下:

打印结果

文章作者: 李佳
文章链接: http://nilsli.com/p/c0a767bd.html
版权声明: 本博客所有文章除特別声明外，均采用 CC BY 4.0 许可协议。转载请注明来源 李佳 !
算法 数据结构 队列
赏
评论
 上一篇
【iOS进阶】-启动优化 【iOS进阶】-启动优化
零、引言用户在移动应用的世界里，第一印象至关重要。对于iOS应用而言，这意味着启动时间必须迅速且流畅。启动优化不仅是提升用户体验的关键，也是展示技术实力的窗口。本文将深入探讨iOS应用的启动过程，分析启动时间的重要性，并提供一系列实用的优化
2020-04-19 李佳
启动优化 调优
下一篇 
【数据结构与算法】-（6）栈 【数据结构与算法】-（6）栈
【数据结构与算法】-（1）基础篇 【数据结构与算法】-（2）线性表基础 【数据结构与算法】-（3）循环链表（单向） 【数据结构与算法】-（4）双向链表和双向循环链表 【数据结构与算法】-（5）链表面试题解析 【数据结构与算法】
2020-04-11 李佳
算法 数据结构 栈 队列
  目录