【数据结构与算法】-（8.3）KMP算法

【数据结构与算法】-（1）基础篇

【数据结构与算法】-（2）线性表基础

【数据结构与算法】-（3）循环链表（单向）

【数据结构与算法】-（4）双向链表和双向循环链表

【数据结构与算法】-（5）链表面试题解析

【数据结构与算法】-（6）栈

【数据结构与算法】-（7）队列

【数据结构与算法】-（8）栈之算法题

【数据结构与算法】-（8.1）字符串去重算法

【数据结构与算法】-（8.2）字符串搜索算法和RK&BP算法

〇、引言

在上篇文章中，我们着重介绍了朴素算法（BF算法）以及RK算法，是否还有更优的选择呢，

一、概念

克努斯-莫里斯-普拉特算法

在计算机科学中，Knuth-Morris-Pratt字符串查找算法（简称为KMP算法）可在一个主文本字符串S内查找一个词W的出现位置。此算法通过运用对这个词在不匹配时本身就包含足够的信息来确定下一个匹配将在哪里开始的发现，从而避免重新检查先前匹配的字符。

这个算法是由高德纳和沃恩·普拉特在1974年构思，同年詹姆斯·H·莫里斯也独立地设计出该算法，最终由三人于1977年联合发表。

二、原理

2.1 回顾BF 算法

再次回顾一下字符串查找的题目，给定一个字符串S = 'abcdbdacd' ，模式串T = 'abcdz'' ，在这个场景下，S 和 T 的前4个字符都相等，从第5个字符开始不等。查找流程，如果所示

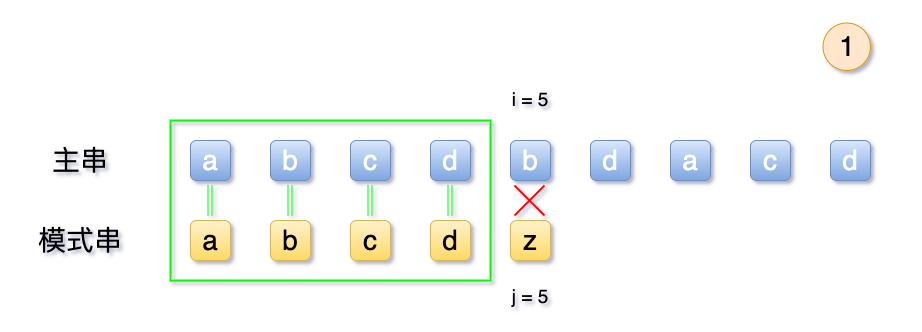
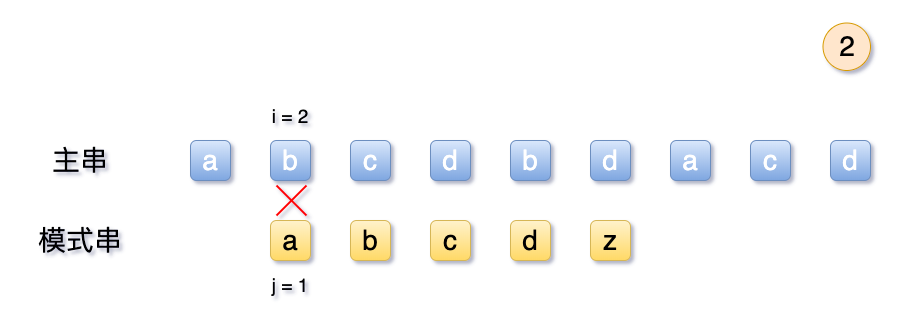
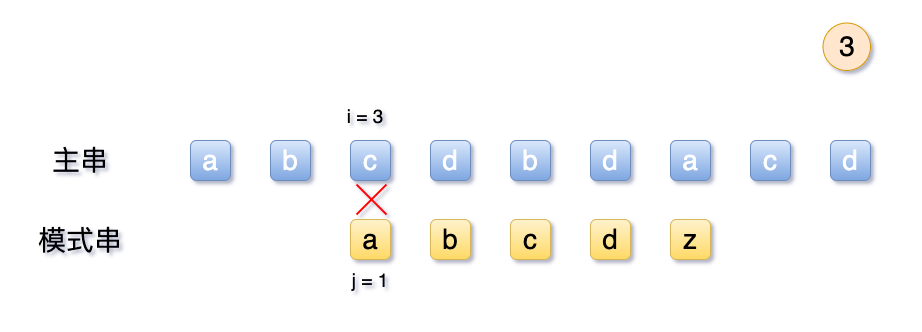
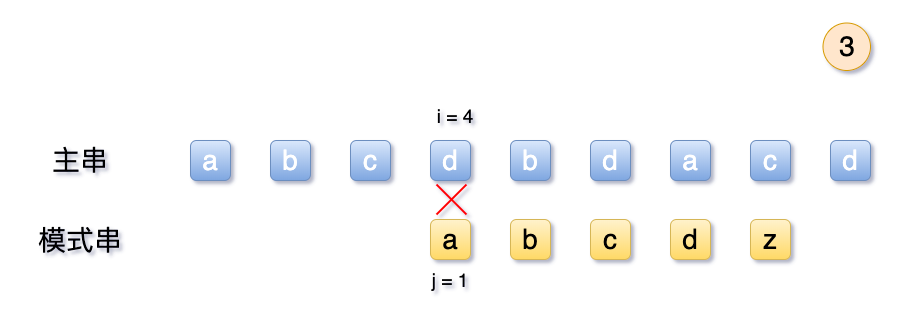
2.2 弊端：无用回溯

从上面可以看到，按照之前的 BF 算法， 也就是朴素算法， 当模式串T 与主串S不一致时候，会将主串的起始序号i 回溯至2，模式串j回溯至1，重新开始匹配。

这样看起来非常有条理，代码写起来也容易看懂，但是是不是有些冗余呢？

这么说吧，给出的条件模式串T 中的 abcdz，第一位a与其他位的字符均不相，那么对比结果后，主串中的S 的首字符a 同样与不相等呢? 那么此时拿T中的首字符a 与S 中前2-5位字符，可以得知，必然都不相等。

那么，是不是可以，将主串S中，确定与模式串T匹配过的那一部分字符跳过——也就是主串的 i 不再进行回溯，而只移动模式串T呢？答案是可以的，不过要分两种情况。

2.3 场景A：模式串T 无重复

看看图所示。

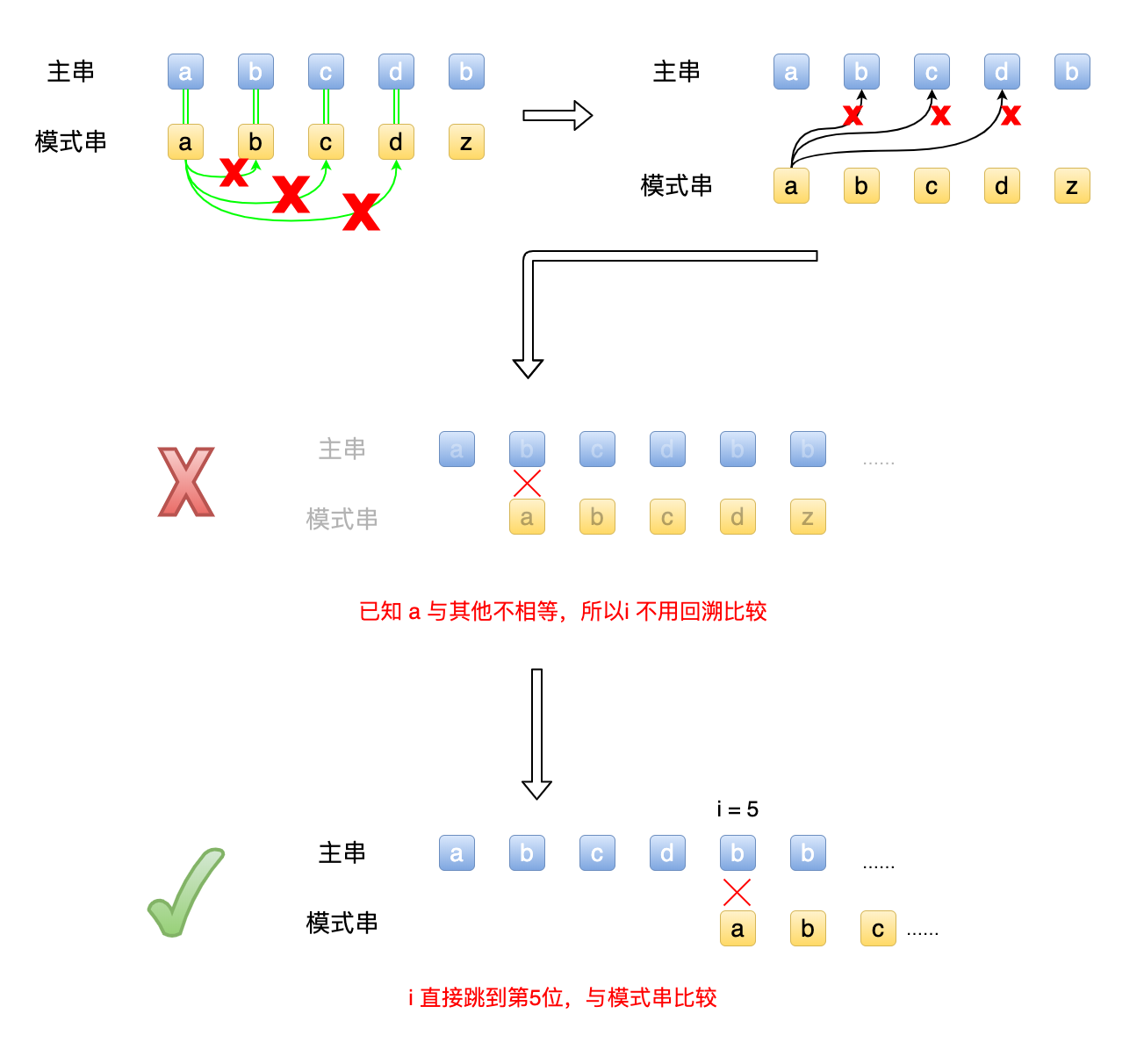
在S 和 T模式串 T 中前4位均匹配，第5位匹配失败。

由于的abcd 均不相等，而第5位失败后，我们可以轻易得知，模式串首位a 与主串的前4位均不相等，故可以直接将主串的 i 移动到第5位与模式串相比。

此时 i 不变，j 回归到1

2.4 场景B：模式串T有重复

那么，如果模式串中，如果有其他字符与a 重复，是不是也可以全部跳过呢？

当然不是。

我们设定一个场景，主串S = abcabd，模式串为T = abcabz

我们通过BF 朴素算法再次排列一下，如图所示

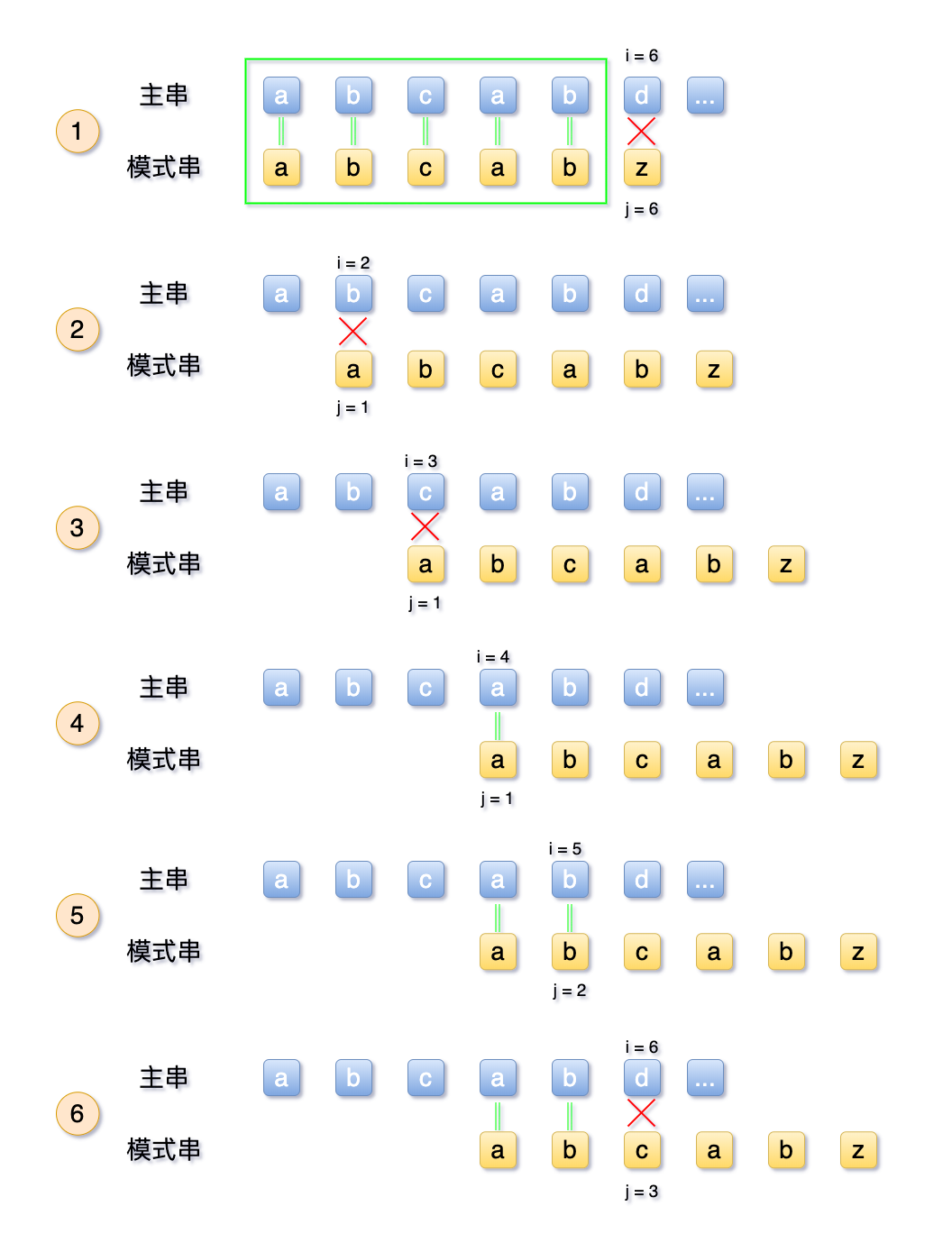
可见，由于模式串中首位a 与第二、三位的b、c 均不相等，所以第2、3步均为多余步骤，可以跳过。

而来到第4步时，由于模式串T 自身有重复的字符，即第1位=第4位，第2位=第5位。

在第1步中，模式串T 的第4位、第5位的a、b 均与 主串的第4、5位匹配过，是一一对应相等的。

那么等于说，第4步中，模式串的首字符a、b，被移动与S 的第4、5位去匹配，也可以省略。

汇总一下：模式串中有与首字符相同的字符，可以跳过一些重复判断步骤。

如下图所示，这样的步骤就可以跳过：

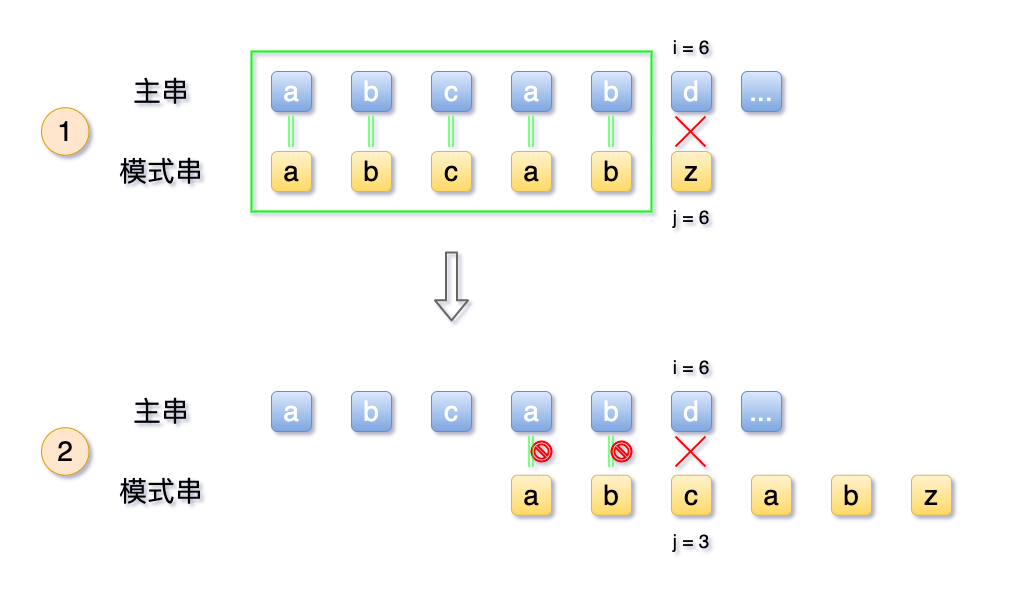
从上图中可以看到，主串的 i是不会像BF算法一样，反复的回溯的， 这也是KMP算法的重要的一点，这样可以省掉一部分的时间复杂度。

2.5 思考归纳

另外，j值的变化也值得寻味。

场景A中，由于模式串没有重复元素，j 从5回到了1 （重复数0）

而在场景B中，由于模式串中的 T = abcabz，ab 是重复的，此时 j 跳到了3（重复数2）。

这里根据反复的思考，得出 j 值变化多少，与重复数量——也就是前缀，后缀相似度有关。

这里KMP算法，引入了一个next 数组，专门用来保管 j值的变化，数组结果如下

究竟是怎么来的，继续探索

2.5 逆推next 数组

探索之前，要牢记一句话：next数组用来保存 j 的变化后的位置。

2.5.1 模式串为：abcdef

j	123456
模式串T	abcdef

1. 当 j = 1 时，next[j] = 1 ，属第一种情况
2. 当 j = 2 时，此时 j 从1位（a）到 j - 1 （b）位中，只有一个字符 ‘a’， 属于其他情况，此时 next[2] = 1
3. 当 j = 3 时，此时 j 从1位（a）到 j - 1 （ab）位中，有2个字符 ‘ab’，但是a、b并不相等，第二种情况并不满足，所以此时 next[3] = 1
4. 当 j = 4 时，此时 j 从1位（a）到 j - 1 （ab）位中，有3个字符 ‘abc’，但是a、b、c并不相等，第二种情况并不满足，所以此时 next[4] = 1
5. 当 j = 5 时，此时 j 从1位（a）到 j - 1 （abcde）位中，有4个字符 ‘abcd’，但是a、b、c、d并不相等，第二种情况并不满足，所以此时 next[5] = 1
6. 于是总结一下得出next 数组为 01111。

j	12345
模式串T	abcde
next[j]	01111

2.5.2 模式串为：abcabf

j	123456
模式串	abcabf

1. 当 j = 1 时，next[j] = 1 ，属第一种情况
2. 当 j = 2 时，此时 j 从1位（a）到 j - 1 （b）位中，只有一个字符 ‘a’， 属于其他情况，此时 next[2] = 1
3. 当 j = 3 时，此时 j 从1位（a）到 j - 1 （ab）位中，有2个字符 ‘ab’，但是a、b并不相等，第二种情况并不满足，所以此时 next[3] = 1
4. 当 j = 4 时，此时 j 从1位（a）到 j - 1 （ab）位中，有3个字符 ‘abc’，但是a、b、c并不相等，第二种情况并不满足，所以此时 next[4] = 1
5. 当 j = 5 时，此时 j 从1位（a）到 j - 1 （abcde）位中，有4个字符 ‘abcd’，第1位、第4位的a相等，所以此时k = 5，即next[5] = 2
6. 当 j = 6 时，此时 j 从1位（a）到 j - 1 （abcde）位中，有4个字符 ‘abcd’，第1位、第4位的a相等，所以此时k = 5，即next[5] = 2
7. 于是总结一下得出next 数组为 011123。

j	123456
模式串	abcabf
next[j]	011123

2.5.3 模式串为：abcbbabc

j	12345678
模式串	abcbbabc

1. 当 j = 1 时，next[j] = 1 ，属第一种情况
2. 当 j = 2 时，此时 j 从1位（a）到 j - 1 （b）位中，只有一个字符 ‘a’， 属于其他情况，此时 next[2] = 1
3. 当 j = 3 时，此时 j 从1位（a）到 j - 1 （ab）位中，有2个字符 ‘ab’，但是a、b并不相等，第二种情况并不满足，所以此时 next[3] = 1
4. 当 j = 4 时，此时 j 从1位（a）到 j - 1 （ab）位中，有3个字符 ‘abc’，但是a、b、c并不相等，第二种情况并不满足，所以此时 next[4] = 1
5. 当 j = 5 时，此时 j 从1位（a）到 j - 1 （abcb）位中，有4个字符 ‘abcb’，虽然第2、第4相等，但是并不满足前缀相等，所以此时k = 5，即next[5] = 1
6. 当 j = 6 时，此时 j 从1位（a）到 j - 1 （abcba）位中，abcba，首位相等，取第一位 + 1，所以此时k = 2，即next[6]] = 2
7. 当 j = 7 时，此时 j 从1位（a）到 j - 1 （abcbab）位中，abcbab，首位相等，取第2位 + 1，所以此时k = 3，即next[7] = 3
8. 当 j = 8 时，此时 j 从1位（a）到 j - 1 （abcbab）位中，abcbab，首位相等，取第3位 + 1，所以此时k = 4，即next[8] = 4

综上所述，这时的next数组为 01111234

j	12345678
模式串	abcbbabc
next[j]	01111234

2.5.4 模式串为：aaaaab

j	123456
模式串	aaaaab

分析如下：

1. 当 j = 1 时，next[j] = 1 ，属第一种情况
2. 当 j = 2 时，当 j = 2 时，此时 j 从1位（a）到 j - 1 （b）位中，只有一个字符 ‘a’， 属于其他情况，此时 next[2] = 1
3. 当 j = 3 时，此时 j 从1位（a）到 j - 1 （aa）位中，有aa 相等，取前面出现的序号+1，得k = 1+1=2，即 next[3] = 2
4. 当 j = 4 时，此时 j 从1位（a）到 j - 1 （aaa）位中，前缀为 aa，后缀也为 aa， 取前面出现的序号+1，得k = 2+1=2，即 next[3] = 3
5. 当 j = 5 时，此时 j 从1位（a）到 j - 1 （aaaa）位中，有aaa ，后缀 aaa，后缀也是 aaa 取前面出现的序号+1，得k = 3+1=4，即 next[3] = 4
6. 当 j = 6 时，此时 j 从1位（a）到 j - 1 （aaaaa）位中，有aaaaa ，后缀 aaaa，后缀也是 aaa 取前面出现的序号+1，得k = 4+1=4，即 next[3] = 5

综上所述，此时的 next 数组为 0123456

j	123456
模式串	aaaaab
next[j]	012345

三、代码实现

3.1 获取next 数组

总结了半天next 数组，现在先来用代码创建一下

先定义一个特定的String 数组，用来装字符数组

typedef char String[MAXSIZE+1]; /*  0号单元存放串的长度 */

void get_nextArray(String T, int *next)
{
  	int i, j;
  	i = 1;
  	j = 0;
  	next[1] = 0;		// 这是第一种情况，初始为0
  
  	while ( i < T[0]) 	// 循环上限为模式串的长度
    {
      	// 比较模式串 T 的前缀后缀俩字符, 
        //若相等，分别递增
      	if( j == 0 || T[i] == T[j])	
        {
           ++i;
           ++j;
          next[i] = j;
        }
   			else
        {
          // 如果不相等， j 回溯回当前
          j = next[j]	;
        }
    }
}

3.2 获取匹配的字符串

拿到了当前的next 数组，现在就把它用起来吧

int getIndexKMP(String S, String T, int pos)
{
  	// s 		= 主串
		// T 		= 模式串
		// pos 	= 最终符合需求的位置
		int i = pos;
  	int j = 1;
  
  	// next 数组的初始化
  	int next[255];
  
  	// 根据模式串，定义出next
  	get_nextArray(T, next);
  
  	// 开始判断
  	while (i <= S[0] && j <= T[0]) 
    {
      	// 主串与字串如果相等，继续
      	if (j == 0 || S[i] == T[j])
        {
          	++i;
          	++j;
        }else{
          
          	// 两者不相等， j 回溯，具体位置为数组中的值
          	j = next[j];
        }
		}
  
  	// 如果 j 的长度大于模式串长度，即已经取得成功
  	if (j > T[0]) 
      	return i - T[0];
  	else
      	return 0;
}

3.3 运行检验

IDE 里操作一下，奥利给！

int main(int argc, const char * argv[]) {
    // insert code here...
    
    printf("第一次查询");
    String S, T;
    StrAssign(S, "cccaababcabc");
    StrAssign(T, "abc");
    int result = getIndexKMP(S, T, 1);
    if (result > 0) {
        printf("在里面的序号为:     %d\n\n", result);
    }else{
        printf("查找失败，主串并无匹配的模式串!\n\n");
    }
    return 0;
}

结果如下：

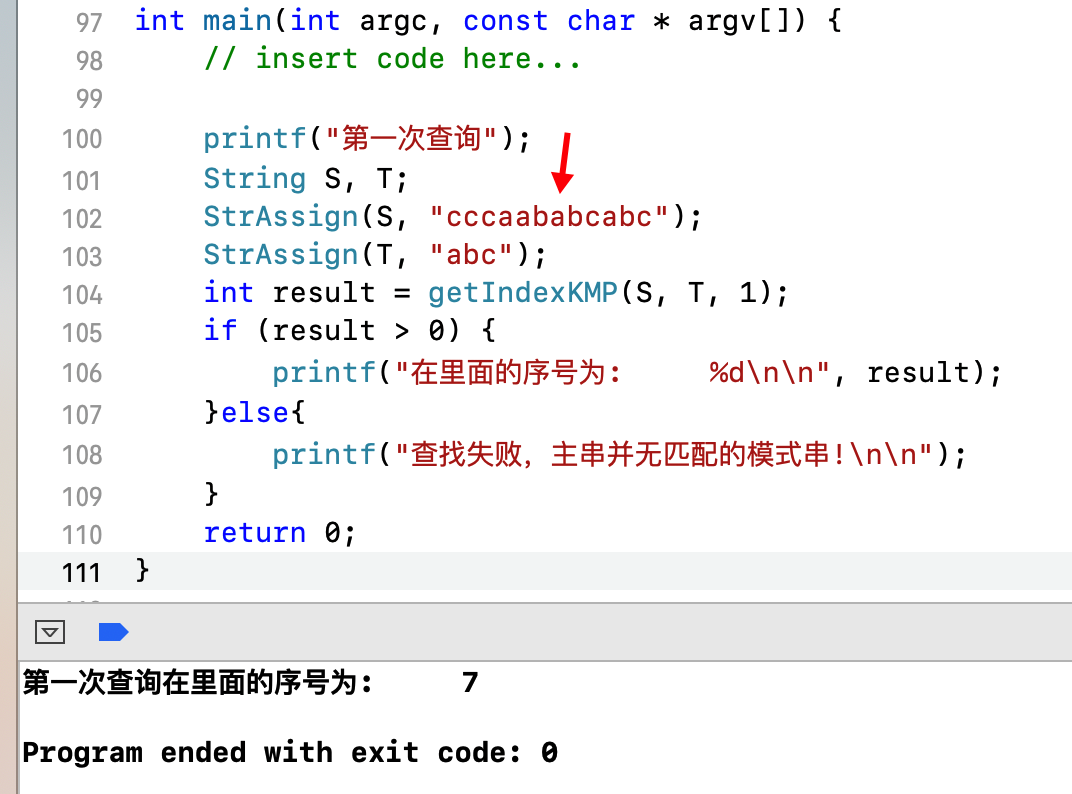
给出的 S = cccaababcabc ， T = abc ，结果是从第7位开始重复，命中！

四、优化改进

4.1 分析不足

上面已经基本实现了KMP算法的时间部分，但是——有些场景还是会有些不理想。

假设给出S = aaaaabcdefgh， 给出的 T = aaaaad

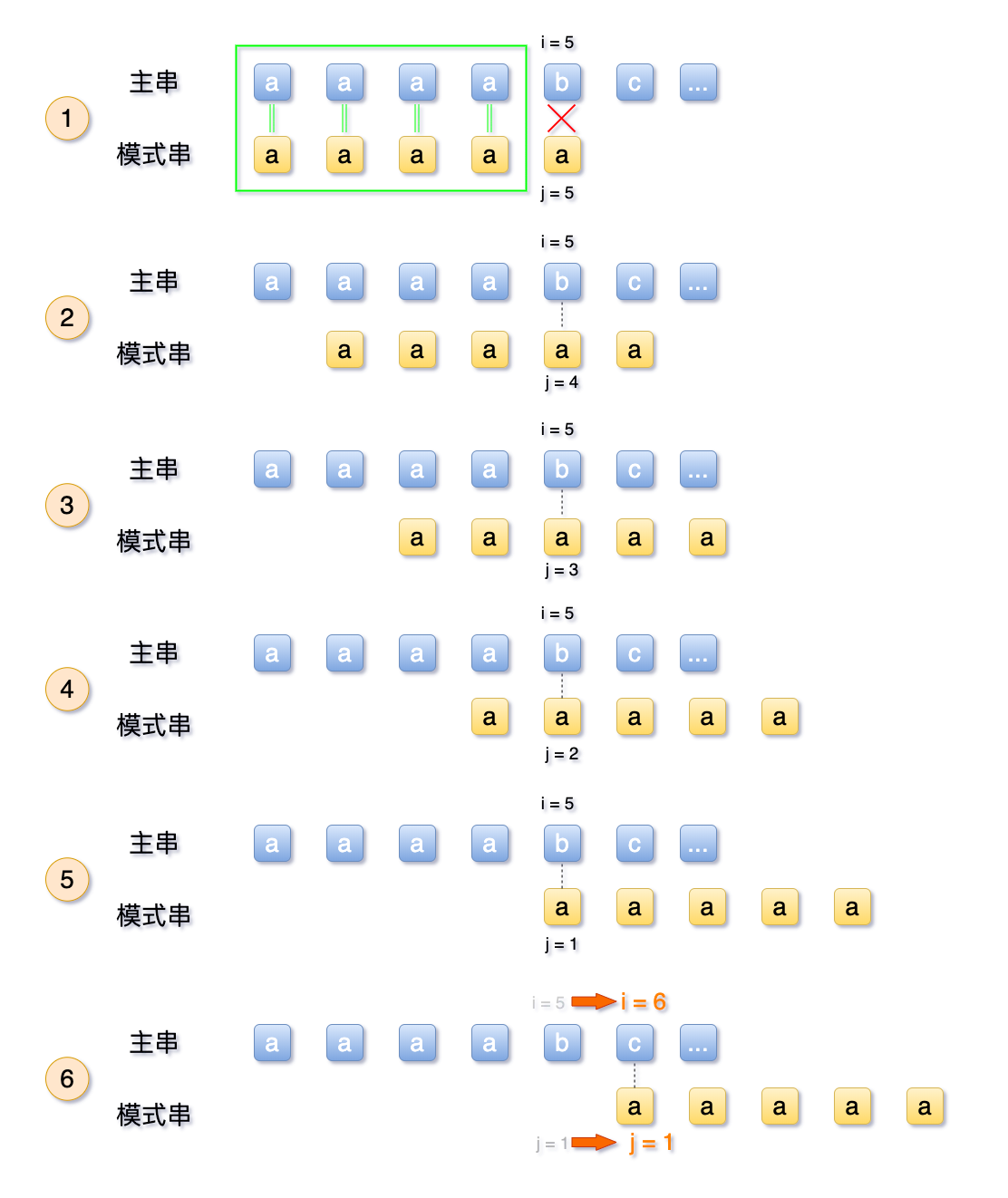
如上图所示，当前4位匹配已知，对比到第5位时，会对 j 进行回溯。

此时 T 的next 数组位 01234，所以j 回溯到 next[5] = 4，即第4位，如第2张图所示。

而此时a 不等于 b，再次回溯，以此类推，一直到第5步，发现回溯完后，T 中的a 一直不等于b，不得不放弃回溯，直接将S 中的 i 增加，跳到下一个字符。

而我们明明看到了，a 中的前5位都是一致的，本来第1步时，模式串中a 不等于主串 中的b， 完全可以放弃2，3，4，5这几部的比较。

4.2 新的nextVal 数组

根据上面的总结，说明之前的next数组有可以改进的地方，改进如下:

void get_nextVal(String T, int *nextVal)
{
      int i, j;
      i = 1;
      j = 0;
      nextVal[1] = 0;        // 这是第一种情况，初始为0
  
      while ( i < T[0])     // 循环上限为模式串的长度
    {
          // 比较模式串 T 的前缀后缀俩字符,
        //若相等，分别递增
          if( j == 0 || T[i] == T[j])
        {
           ++i;
           ++j;
            if (T[i] == T[j]) {
                nextVal[i] =  nextVal[j];
            }else{
                nextVal[i] = j;
            }
        }
               else
        {
          // 如果不相等， j 回溯回当前
          j = nextVal[j] ;
        }
    }
}

可以看到，在判断前后缀相同的时候，添加了这一段判断

if (T[i] == T[j]) 
    nextVal[i] = nextVal[j];

这里的的意思是：

判断——如果当前 T 中的i 位字符与 T 的i位字符相等，且两串的各自下一个字符还是一一相等，把T中前缀的值——即上一次匹配 的的next 值，放入新的nextVal 数组中。

4.3逆推nextVal数组

声明比较的规则，即拿

左边 = T[j]

右边 = T [next[j]]

两者相比较！

4.3.1 模式串为：ababaaaba

j	123456789
模式串	ababaaaba
next[j]	011234223
nextVal[j]	010104210

1. j = 1, nextVal[1] = 0;
2. j = 2, 照旧。左边为T [2] = b，右边 T[next[2]] = T[1] = a 这种前后字符不相等，还是沿用之前next[i] 的逻辑，即 = 1；
3. j = 3，此时为新情况，左边为T [3] = a，右边 T[next[3]] = T[1] = a 这种前后字符相等，使用新逻辑：nextVal[3] = nextVal[1] = 0；
4. j = 4 ，此时为新情况，左边为T [4] = b，右边 T[next[4]] = T[2] = b 这种前后字符相等，使用新逻辑：nextVal[4] = nextVal[2] = 1；
5. j = 5，此时为新情况，左边为T [5] = a，右边 T[next[5]] = T[3] = a 这种前后字符相等，使用新逻辑：nextVal[5] = nextVal[3] = 0；
6. j = 6，照旧。左边为T [6] = a，右边 T[next[6]] = T[4] = b 这种前后字符不相等，还是沿用之前next[i] 的逻辑，即 = 4；
7. j = 7，照旧。左边为T [7] = a，右边 T[next[7]] = T[2] = b 这种前后字符不相等，还是沿用之前next[i] 的逻辑，即 = 2；
8. j = 8，此时为新情况，左边为T [8] = b，右边 T[next[8]] = T[2] = b 这种前后字符相等，使用新逻辑：nextVal[8] = nextVal[2] = 1；
9. j = 9，此时为新情况，左边为T [9] = a，右边 T[next[9]] = T[3] = a 这种前后字符相等，使用新逻辑：nextVal[9] = nextVal[3] = 0；

4.3.2 模式串为：aaaacd

j	123456
模式串	aaaaad
next[j]	012345
nextValue[j]	000005

现在回到引起需要改进的字符串里面来，aaaaad，依次分析

1. j = 1, nextVal[1] = 0;

2. j = 2, 此时为新情况，左边为T [2] = a，右边 T[next[2]] = T[1] = a 这种前后字符相等，使用新逻辑：nextVal[2] = nextVal[1] = 0；

3. j = 3，此时为新情况，左边为T [3] = a，右边 T[next[3]] = T[2] = a 这种前后字符相等，使用新逻辑：nextVal[3] = nextVal[2] = 0；

4. 同上累加

5. 同上累加

6. 同上累加

7. j = 6，此时照旧。左边T[6] = d， 右边 T [next[6]] = T [5] = a， 两者并不相等，沿用之前的next，即 nextVal[6] = 5

4.4 改进小结

总之，这里改进了的一句代码

if (T[i] == T[j]) { nextVal[i] = nextVal[j];}

最终的含义：

是如果存在某个字符a，如果它当前next位指向的字符相等—— 它的偏移值nextVal 数组当前的值，就使用会沿用指向的那个值的nextVal值。其他情况的逻辑照旧。

画了个图解释一下：

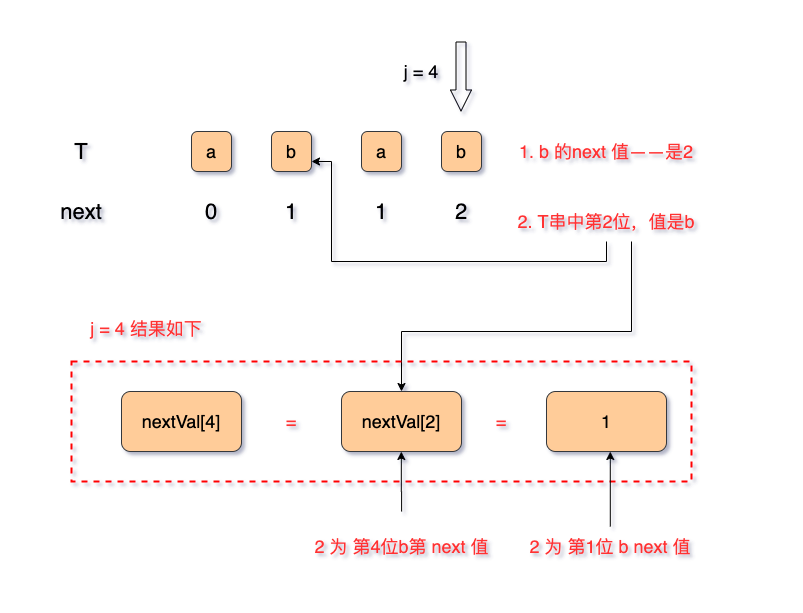
相关实现代码，放在GITHUB 上，欢迎食用 XD!