引言
字符串搜索算法(String searching algorithms)
又称字符串比对算法(string matching algorithms)是一种搜索算法,是字符串算法中的一类,用以试图在一长字符串或文章中,找出其是否包含某一个或多个字符串,以及其位置。
题目:字符串匹配
给你一个仅包含小写字母的字符串主串S = abcacabdc, 模式串 T= abd, 请查找出模式串在主串第一次出现的位置;提示:主串和模式串均为小写字母且都是合法输入
一、BF算法
1.1 概念
Brute-Force算法,简称为 BF算法,是一种简单朴素的模式匹配算法,常用于在一个主串 S 内查找一个子串 T 的出现位置。
1.2 思路
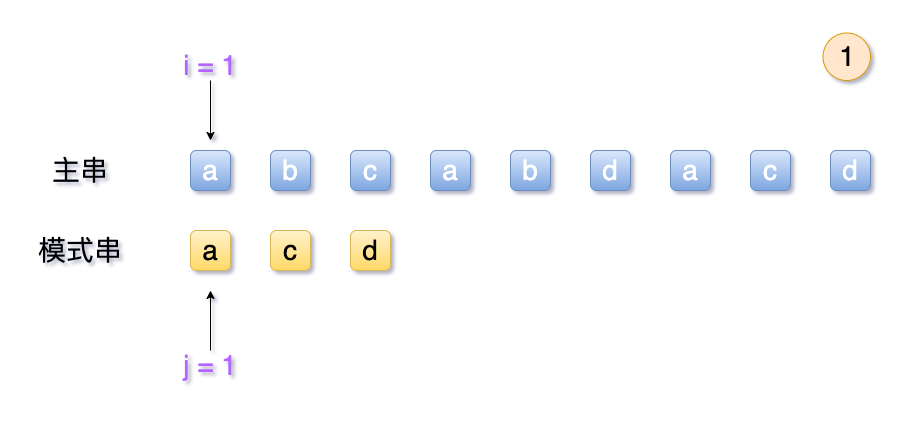
- 排列两个串,对其内部字符进行逐一比较
- 首先对
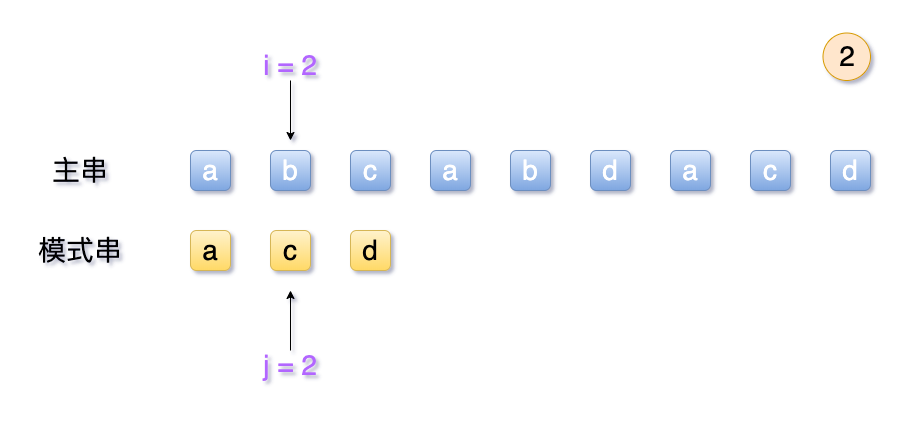
S[1]和T[1]比较,如果相等则跳到S[2]和T[2],两者下标各加1 - 如果
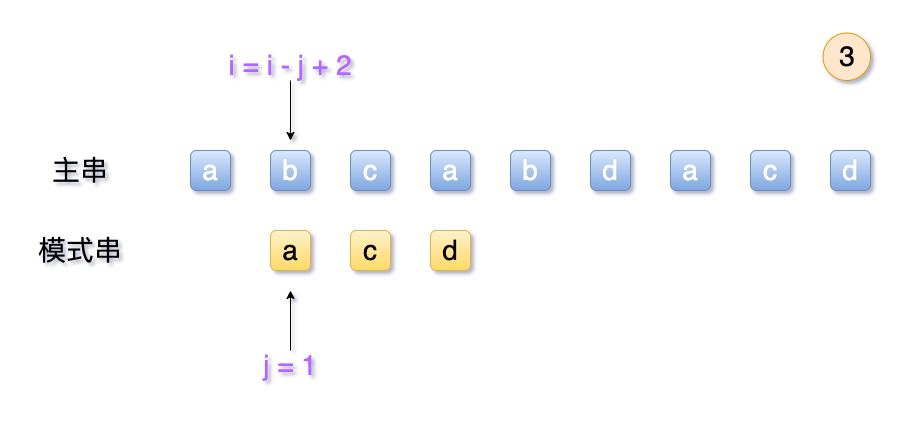
S[i]和T[j]不相等:- 主串的待选次序
i回退到之前j的下一位,即是i = i - j + 2 j退回到第1位
- 主串的待选次序
- 匹配成功条件:字串每一个字符都匹配完,即
j > T[0]。此时,主串位置i即为所得

1.3 代码实现:
字符生成字符串
T/* 生成一个其值等于chars的串T */
Status StrAssign(String T,char *chars)
{
int i;
if(strlen(chars)>MAXSIZE)
return ERROR;
else
{
T[0]=strlen(chars);
for(i=1;i<=T[0];i++)
T[i]=*(chars+i-1);
return OK;
}
}清除字符串
SStatus ClearString(String S)
{
S[0]=0;/* 令串长为零 */
return OK;
}输出字符串里的字符
void StrPrint(String T)
{
int i;
for(i=1;i<=T[0];i++)
printf("%c",T[i]);
printf("\n");
}输出
Next数组的值void NextPrint(int next[],int length)
{
int i;
for(i=1;i<=length;i++)
printf("%d",next[i]);
printf("\n");
}返回字符串
s的元素个数int StrLength(String S)
{
return S[0];
}执行算法内容
int Index_BF(String S, String T,int pos){
//i用于主串S中当前位置下标值,若pos不为1,则从pos位置开始匹配
int i = pos;
//j用于子串T中当前位置下标值
int j = 1;
//若i小于S的长度并且j小于T的长度时,循环继续
while (i <= S[0] && j <= T[0]) {
//比较的2个字母相等,则继续比较
if (S[i] == T[j]) {
i++;
j++;
}else{
//不相等,则指针后退重新匹配
//i 退回到上次匹配的首位的下一位;
//加1,因为是子串的首位是1开始计算;
//再加1的元素,从上次匹配的首位的下一位;
i = i-j+2;
//j 退回到子串T的首位
j = 1;
}}
//如果j>T[0],则找到了匹配模式
if (j > T[0]) {
//i母串遍历的位置 - 模式字符串长度 = index 位置
return i - T[0];
}else{
return -1;
}
}验证算法内容:
int main(int argc, const char * argv[]) {
int i,*p;
String s1,s2;
StrAssign(s1, "abcdex");
printf("s1子串为");
StrPrint(s1);
StrAssign(s2, "xe");
printf("s2子串为");
StrPrint(s2);
i = Index_BF(s1, s2, 1);
printf("i = %d\n",i);
return 0;
}结果验证:
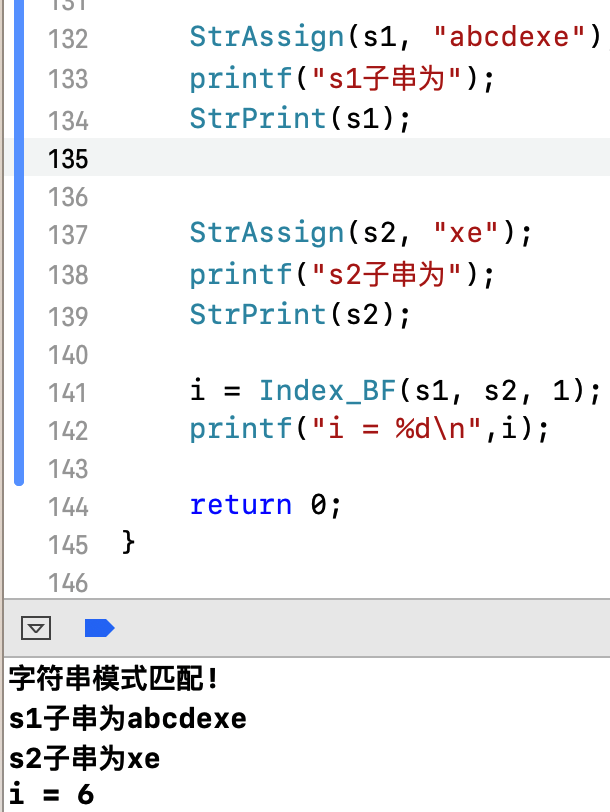
1.4 时间复杂度
但是此直观算法较为暴力,复杂度达到了O(mn),其中 S 的长度为n,T 的长度为m, 所以我们要考虑更快速的算法。
二、RK算法
2.0 概念
RK 算法(Rabin–Karp algorithm )是一个字符串查找算法,由Richard M. Karp and Michael O. Rabin 在1987年提出,使用哈希算法,来比对字符串。
在这里,与粗暴简单的BF 算法不一样,我们引入了哈希值来进行比对,这样计算机只需要匹配整形,相比匹配字符串,更快一些。
散列函数(英语:Hash function)又称散列算法、哈希函数,是一种从任何一种数据中创建小的数字“指纹”的方法。
散列函数把消息或数据压缩成摘要,使得数据量变小,将数据的格式固定下来。该函数将数据打乱混合,重新创建一个叫做散列值(hash values,hash codes,hash sums,或hashes)的指纹。散列值通常用一个短的随机字母和数字组成的字符串来代表。好的散列函数在输入域中很少出现散列冲突。在散列表和数据处理中,不抑制冲突来区别数据,会使得数据库记录更难找到。
2.1 思路:
主串分解成多个字串,用子串与模式串进行核对
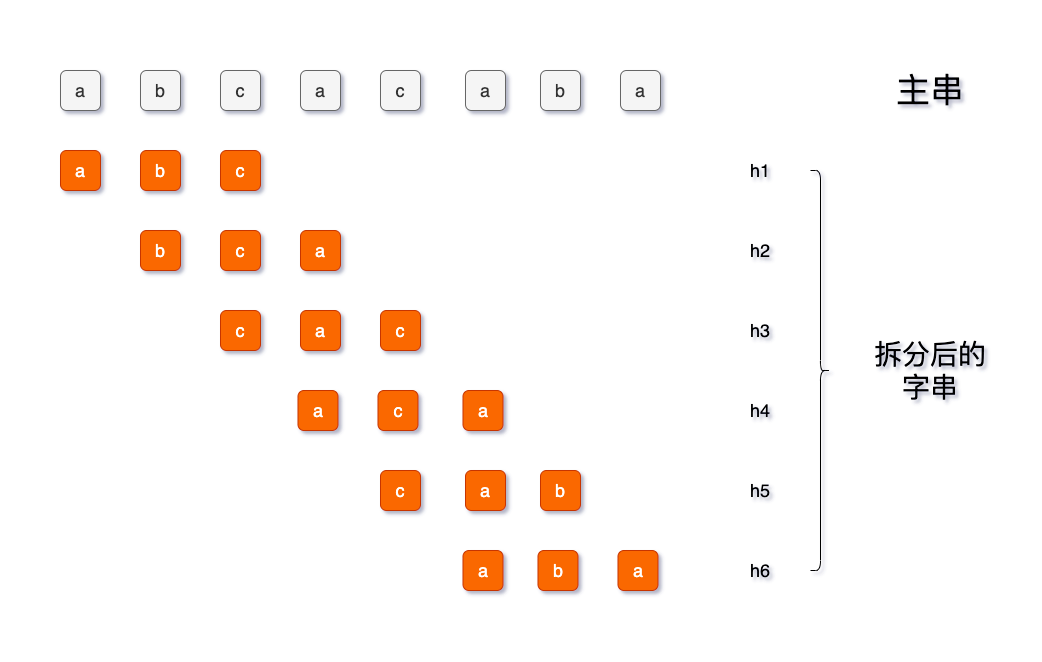
把需要匹配的字符串,转换成
hash值以 a 为基点,将字符与
a的ASCII 码的差值,转换成整形:如abc,结果为
Result= ( a - ‘a’ ) * 262 + (b - ‘a’ ) * 26 + (c - ‘a’ )
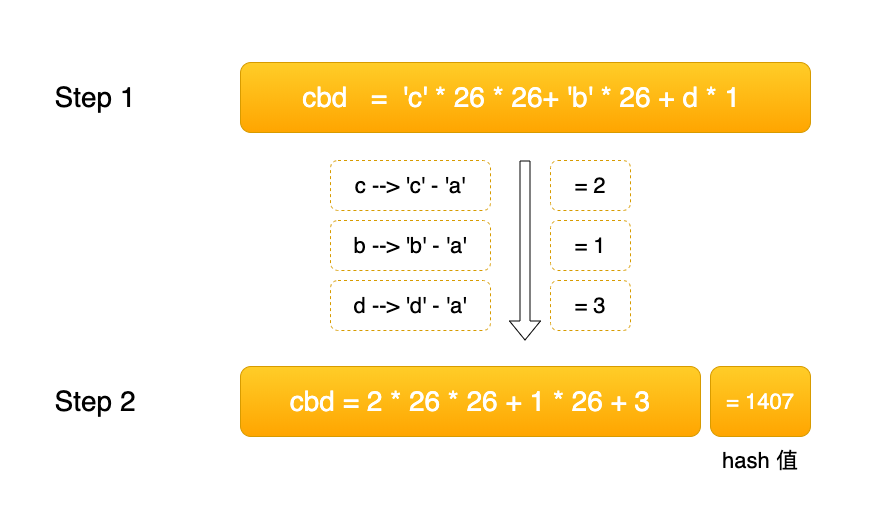
用主串对字串和模式串的的
hash值来互相判断,更为高效
2.2 代码实现
二次确认
hash值相等。以防止有的字符串相同,但是hash不相等。int isMatch(char *S, int i, char *P, int m)
{
int is, ip;
for(is=i, ip=0; is != m && ip != m; is++, ip++)
if(S[is] != P[ip])
return 0;
return 1;
}算出 d 进制下的最高位:
int getMaxValue(int m){
int h = 1;
for(int i = 0;i < m - 1;i++){
h = (h*d);
}
return h;
}进行RK 进入查询
int RK(char *S, char *P)
{
//1. n:主串长度, m:子串长度
int m = (int) strlen(P);
int n = (int) strlen(S);
printf("主串长度为:%d,子串长度为:%d\n",n,m);
//A.模式串的哈希值; St.主串分解子串的哈希值;
unsigned int A = 0;
unsigned int St = 0;
//2.求得子串与主串中0~m字符串的哈希值[计算子串与主串0-m的哈希值]
//循环[0,m)获取模式串A的HashValue以及主串第一个[0,m)的HashValue
//此时主串:"abcaadddabceeffccdd" 它的[0,2)是ab
//此时模式串:"cc"
//cc = 2 * 26^1 + 2 *26 ^0 = 52+2 = 54;
//ab = 0 * 26^1 + 1 *26^0 = 0+1 = 1;
for(int i = 0; i != m; i++){
//第一次 A = 0*26+2;
//第二次 A = 2*26+2;
A = (d*A + (P[i] - 'a'));
//第一次 st = 0*26+0
//第二次 st = 0*26+1
St = (d*St + (S[i] - 'a'));
}
//3. 获取d^m-1值(因为经常要用d^m-1进制值)
int hValue = getMaxValue(m);
//4.遍历[0,n-m], 判断模式串HashValue A是否和其他子串的HashValue 一致.
//不一致则继续求得下一个HashValue
//如果一致则进行二次确认判断,2个字符串是否真正相等.反正哈希值冲突导致错误
//注意细节:
//① 在进入循环时,就已经得到子串的哈希值以及主串的[0,m)的哈希值,可以直接进行第一轮比较;
//② 哈希值相等后,再次用字符串进行比较.防止哈希值冲突;
//③ 如果不相等,利用在循环之前已经计算好的st[0] 来计算后面的st[1];
//④ 在对比过程,并不是一次性把所有的主串子串都求解好Hash值. 而是是借助s[i]来求解s[i+1] . 简单说就是一边比较哈希值,一边计算哈希值;
for(int i = 0; i <= n-m; i++){
if(A == St)
if(isMatch(S,i,P,m))
//加1原因,从1开始数
return i+1;
St = ((St - hValue*(S[i]-'a'))*d + (S[i+m]-'a'));
}
return -1;
}
2.3 代码验证
执行查找代码
int main()
{
char *buf="abcababcabx";
char *ptrn="abcabx";
printf("主串为%s\n",buf);
printf("子串为%s\n",ptrn);
int index = RK(buf, ptrn);
printf("find index : %d\n",index);
return 1;
}结果如下:

2.4 复杂度
- 时间复杂度:O(n+m),最坏O((n-m) * m)
- 空间复杂度:O(1)



